
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
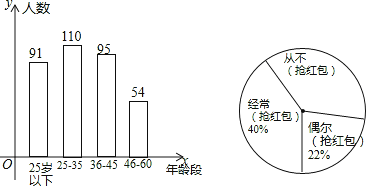
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
【答案】(1)25-35之间;(2)217人;1520人.
【解析】试题分析:(1)根据中位数的定义,中位数是大小处于中间位置的数,根据定义即可作出判断;
(2)利用调查的职工的人数350乘以对应的百分比即可求得“参与抢红包”的人数;
利用总人数4000乘以“从不(抢红包)”的比例即可求得“从不(抢红包)”的人数.
试题解析:(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是25-35之间;
(2)“经常(抢红包)”和“偶尔(抢红包)”共占的百分比为40%+22%=62%,
则这次接受调查的职工中“参与抢红包”的人数是350×62%=217(人);
根据题意得:4000×(1-40%-22%)=1520(人),
则该企业“从不(抢红包)”的人数是1520人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若关于的x一元二次方程kx2–2x–1=0有两个不相等的实数根,则k的取值范围是( )
A. k >–1 B. k >–1且k ≠0 C. k <1 D. k <1,且k ≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数精确到百万位用科学记数法表示正确的是( )
A. 6.80×107 B. 6.8×108 元 C. 6.80×108元 D. 6.8×106元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一定的条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当t=4秒时,该物体所经过的路程为( )
A. 28米 B. 48米 C. 68米 D. 88米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,-1),与x轴交于A、B两点.
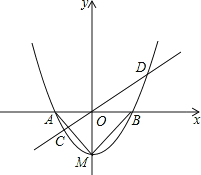
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 4 | 2 | 5 | 1 |
这此测试成绩的中位数和众数分别为( )
A. 47,49 B. 47.5,49 C. 48,49 D. 48,50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com