
【题目】如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,-1),与x轴交于A、B两点.
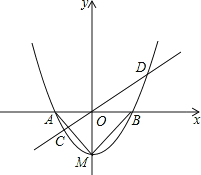
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.
【答案】(1)y=x2-1.(2)△MAB是等腰直角三角形.理由见解析;(3)MC⊥MD;理由见解析.
【解析】试题分析:(1)待定系数法即可解得.
(2)由抛物线的解析式可知OA=OB=OM=1,得出∠AMO=∠MAO=∠BMO=∠MBO=45°从而得出△MAB是等腰直角三角形.
(3)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2-1),C(n,n2-1),通过EG∥DH,得出![]() ,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠DMH=90°,即可求得结论.
,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠DMH=90°,即可求得结论.
试题解析:(1)∵抛物线y=x2+bx+c的顶点坐标为M(0,-1),
∴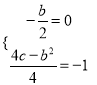 ,解得b=0,c=-1,
,解得b=0,c=-1,
∴抛物线的解析式为:y=x2-1.
(2)△MAB是等腰直角三角形.
由抛物线的解析式为:y=x2-1可知A(-1,0),B(1,0),
∴OA=OB=OM=1,
∴∠AMO=∠MAO=∠BMO=∠MBO=45°,
∴∠AMB=∠AMO+∠BMO=90°,AM=BM,
∴△MAB是等腰直角三角形.
(3)MC⊥MD;
分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC延长线于G,交DF于H,
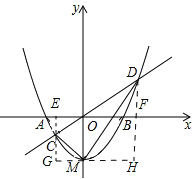
设D(m,m2-1),C(n,n2-1),
∴OE=-n,CE=1-n2,OF=m,DF=m2-1,
∵OM=1,
∴CG=n2,DH=m2,
∵EG∥DH,
∴![]() ,
,
即![]() ,
,
m(1-n2)=-n(m2-1),
m-mn2=-m2n+n,
(m2n-mn2)=-m+n,
mn(m-n)=-(m-n),
∴mn=-1
解得m=-![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MD.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】将下列多项式因式分解,结果中不含有因式(x-2)的是( )
A. x2-4 B. x3-4x2-12x C. x2-2x D. (x-3)2+2(x-3)+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
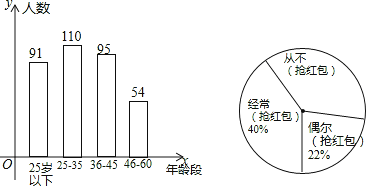
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
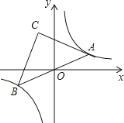
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com