
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。如对于任意正实数![]() 、x,可作变形:x+=(-
、x,可作变形:x+=(-![]() )2+2,因为(-
)2+2,因为(-![]() )2≥0,所以x+≥2(当x=时取等号).
)2≥0,所以x+≥2(当x=时取等号).
记函数y=x+(a>0,x>0),由上述结论可知:当x=时,该函数有最小值为2.
直接应用: 已知函数y1=x(x>0)与函数y2 = (x>0),则当x= 时,y1+y2取得最小值为 .
变形应用: 已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求 的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①、求y关于x的函数关系式(写出自变量x的取值范围);
②、求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
科目:初中数学 来源: 题型:
【题目】从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合用全面调查的是( )
A. 调査某批次汽车的抗撞击能力 B. 鞋厂检测生产鞋底能承受的弯折次数
C. 了解某班学生的身髙情况 D. 调査市场上某种贪品的色素含量是否符备国家标准
查看答案和解析>>
科目:初中数学 来源: 题型:
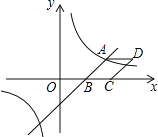
【题目】如图,已知一次函数y=![]() x-3与反比例函数
x-3与反比例函数![]() 的图象相交于点A
的图象相交于点A![]() ,与x轴相交于点B.
,与x轴相交于点B.
(1)填空:![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com