
 ,得到如图2、如图三情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图二证明你的判断.
,得到如图2、如图三情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图二证明你的判断.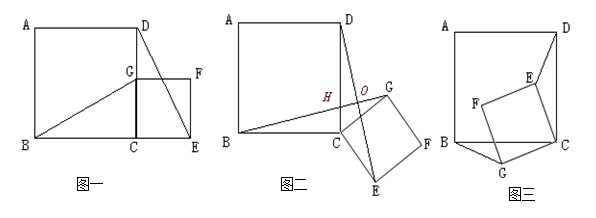
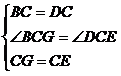 =90°
=90° =90°
=90°

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
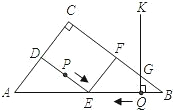 ,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
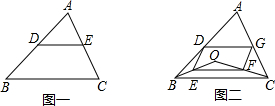 如图一,三角形ABC中,D、E分别为AB、AC的中点.
如图一,三角形ABC中,D、E分别为AB、AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
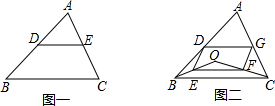 如图一,三角形ABC中,D、E分别为AB、AC的中点.
如图一,三角形ABC中,D、E分别为AB、AC的中点.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com