【题目】画抛物线y=x2﹣2x﹣3的草图，并说出开口方向，对称轴，顶点坐标，增减性，最值．
【答案】见解析
【解析】试题分析：
（1）画二次函数图象，至少要描出5个点，其中顶点坐标必取，与坐标轴的交点，如果有，建议取，所取点，尽量在对称轴两边对称选取，否则图象不对称不完整.
（2）a大小决定开口方向，而a=1>0，故开口向上；对称轴为直线
，顶点为
即（1，-4）； 令x=0，则y=-3，得与y轴交点（0，-3）；令y=0,得方程x2﹣2x﹣3=0，解之得
，得与x轴两个交点（3,0），（-1,0）.
（3）列表后描点，然后用平滑曲线连接各点，就得所求作的图象.
（4）根据草图，增减性，最值就一目了然.
解：列表，如下：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
描点、连线，如图所示．
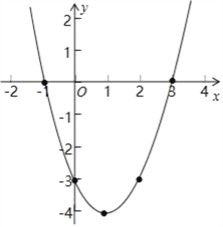
观察函数图象，可知：抛物线开口向上；对称轴为直线x=1；顶点坐标为（1，﹣4）；当x＜1时，y随x增大而减小，当x＞1时，y随x增大而增大；抛物线y=x2﹣2x﹣3存在最小值，最小值为﹣4．
智趣暑假温故知新系列答案科目：初中数学 来源： 题型：
【题目】一座桥如图，桥下水面宽度AB是20米，高CD是4米．要使高为3米的船通过，则其宽度须不超过多少米．
（1）如图1，若把桥看做是抛物线的一部分，建立如图坐标系．
①求抛物线的解析式；
②要使高为3米的船通过，则其宽度须不超过多少米？
（2）如图2，若把桥看做是圆的一部分．
①求圆的半径；
②要使高为3米的船通过，则其宽度须不超过多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=﹣x+5的图象与反比例函数
（k≠0）在第一象限的图象交于A（1，n）和B两点．
（1）求反比例函数的解析式及点B坐标；
（2）在第一象限内，当一次函数y＝－x＋5的值大于反比例函数
（k≠0）的值时，写出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小丽想知道自家门前小河的宽度，于是她按以下办法测出了如下数据：小丽在河岸边选取点A，在点A的对岸选取一个参照点C，测得∠CAD=30°；小丽沿岸向前走30m选取点B，并测得∠CBD=60°．请根据以上数据，用你所学的数学知识，帮小丽计算小河的宽度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1,在平面直角坐标系中,A（a,0）是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B（0,b）,且(a-3)2+|b+4|=0,S四边形AOBC=16．
（1）求C点坐标；
（2）如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数．
（3）如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化？若不变,求出其值,若变化,说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG//DB交CB的延长线于G．
（1）求证：△ADE≌△CBF；
（2）若四边形BEDF是菱形，求证四边形AGBD是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．
（1）如图①，当α=90°时，求AE′，BF′的长；
（2）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；
（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．
解：∵∠1+∠EFD=180°（邻补角定义），∠1+∠2=180°（已知 ）
∴ （同角的补角相等）①
∴ （内错角相等，两直线平行）②
∴∠ADE=∠3（ ）③
∵∠3=∠B（ ）④
∴ （等量代换）⑤
∴DE∥BC（ ）⑥
∴∠AED=∠C（ ）⑦
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
