(1)解:120;
(2)证明:∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠DCB=∠DCB+∠BCE
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
(3)解:①当点D在线段AM上(不与点A重合)时(图1),

由(2)可知△ACD≌△BCE,
则∠CBE=∠CAD=30°,作CH⊥BE于点H,
则PQ=2HQ,连接CQ,则CQ=5.
在Rt△CBH中,∠CBH=30°,BC=AB=8,则
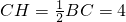
.
在Rt△CHQ中,由勾股定理得:
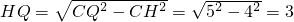
,
则PQ=2HQ=6
②当点D在线段AM的延长线上时(图2),
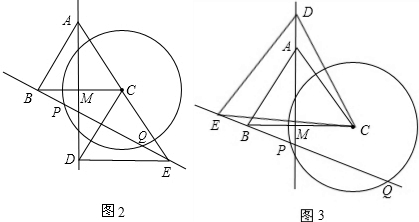
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACB+∠DCB=∠DCB+∠DCE
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
∴∠CEB=∠CDA=30°
同理可得:PQ=6.
③当点D在线段MA的延长线上时(图3),
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠ACE=∠BCE+∠ACE=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD
∵∠CAM=30°
∴∠CBE=∠CAD=150°
∴∠CBQ=30°
同理可得:PQ=6
综上所述,PQ的长是6.
分析:(1)三角形内角和是180°,等边三角形的内角都相等,所以,其中一个内角的度数是180°÷3,结合图形可求得∠ACB=∠DCE=60°,从而可得∠ACE的度数;
(2)根据等边三角形的性质,利用SAS求证△ADC≌△BEC;
(3)①当点D在线段AM上(不与点A重合)时,作Rt△CBH,在直角三角形中,利用勾股定理求得;②当点D在线段AM的延长线上时,求证△ACD≌△BCE,然后求值;③当点D在线段MA的延长线上时,求证△ACD≌△BCE后求值.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA无法证明三角形全等.

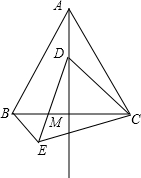 方作等边△CDE,连接BE.
方作等边△CDE,连接BE.
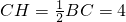 .
.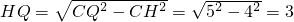 ,
,


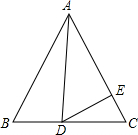 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( ) 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: