
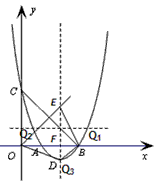
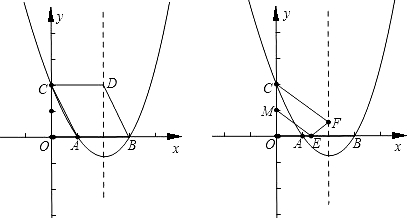
 交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D。
交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D。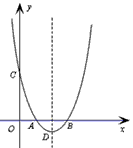
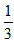 ?若存在,求点Q的坐标;若不存在,请说明理由。
?若存在,求点Q的坐标;若不存在,请说明理由。| 解:(1)求出:b=-4,c=3,抛物线的对称轴为:x=2; (2)抛物线的解析式为  ,易得C点坐标为(0,3),D点坐标为(2,-1), ,易得C点坐标为(0,3),D点坐标为(2,-1),设抛物线的对称轴DE交x轴于点F,易得F点坐标为(2,0), 连接OD,DB,BE, ∵△OBC是等腰直角三角形,△DFB也是等腰直角三角形,E点坐标为(2,2), ∴∠BOE=∠OBD=45°, ∴OE∥BD, ∴四边形ODBE是梯形, 在Rt△ODF和Rt△EBF中, OD= 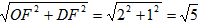 ,BE= ,BE=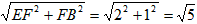 , ,∴OD=BE, ∴四边形ODBE是等腰梯形; (3)存在, 由题意得: 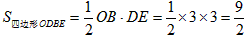 , ,设点Q坐标为(x,y), 由题意得: 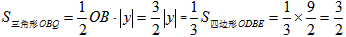 , ,∴  , ,当y=1时,即  , ,∴ 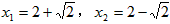 , ,∴Q点坐标为(2+  ,1)或(2- ,1)或(2- ,1), ,1),当y=-1时,即 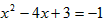 ,∴x=2, ,∴x=2,∴Q点坐标为(2,-1), 综上所述,抛物线上存在三点Q1(2+ 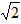 ,1),Q2(2- ,1),Q2(2-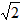 ,1),Q3(2,-1), ,1),Q3(2,-1),使得 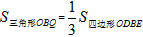 。 。 |
 |


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届浙江省杭州市上城区中考二模数学试卷(带解析) 题型:解答题
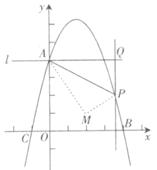
已知抛物线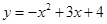 交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.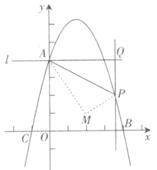
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市上城区中考二模数学试卷(解析版) 题型:解答题
已知抛物线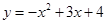 交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com