
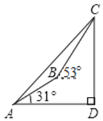
【题目】鄂州市电信部门积极支持鄂州国际航空大都市的建设,如图,计划修建一条连接B,C两地的电缆,测量人员在山脚A测得B,C两地的仰角分别为31°和45°,在B处测得C处的仰角为53°.已知C地比A地髙50m,则电缆BC至少需要多少米?(精确到1m,参考数据:sin31°≈![]() ,tan31°≈
,tan31°≈![]() ,sin37°≈0.6,cos37°≈0.8)
,sin37°≈0.6,cos37°≈0.8)
【答案】45.5米
【解析】
过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.设BC=xm,用x表示出BE、CE,根据题意求出AF、BF,根据正切的定义列出算式,求出x即可解答本题.
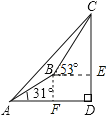
解:作BE⊥CD于点E,作BF⊥AD于点F,如图所示,
由题意可得,
∠CAD=45°,∠BAF=31°,∠CBE=53°,∠ADC=90°,CD=50m,
∴∠ACD=45°,∠BCE=37°,AD=CD=50m,
设BC=xm,
则BE=BCsin37°=xsin37°,CE=xcos37°,
∴DF=BE=xsin37°,
∴AF=50-xsin37°,
∴BF=AFtan31°=(50-xsin37°)tan31°,
∵BF=DE,
∴(50-xsin37°)tan31°=50-xcos37°,
解得,x≈45.5
答:电缆BC至少需要45.5米.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BC=CD,∠C=2∠BAD.
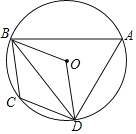
(1)求∠BOD的度数;
(2)求证:四边形OBCD是菱形;
(3)若⊙O的半径为r,∠ODA=45°,求△ABD的面积(用含r的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
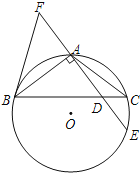
【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.若AF=3,tan∠ABD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
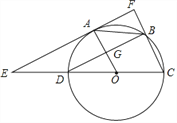
【题目】如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形。过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)求证:EF是⊙O的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
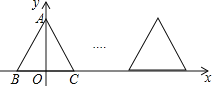
【题目】已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程![]() ,
,
(1)求证:方程一定有两个不相等的实数根;
(2)![]() 取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
(3)![]() 取何值时方程的两个根异号且负的实数根的绝对值大.
取何值时方程的两个根异号且负的实数根的绝对值大.
查看答案和解析>>
科目:初中数学 来源: 题型:
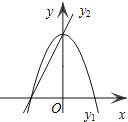
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.那么使得M=1的x值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com