
 青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)
青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)分析 (1)到线段两个端点距离相等的点应在线段的垂直平分线上,所以应作出任意两条线段的垂直平分线;
(2)连接点P和各顶点,以及AC.根据线段的垂直平分线的性质和三角形的内角和定理求解.
解答 解:(1)如图,P点即为所求;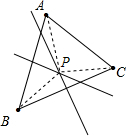
(2)连接点P和各顶点,以及AC.
∵PA=PB,
∴∠PAB=∠PBA,
同理∠PAC=∠PCA,
∵∠BAP+∠PAC=∠BAC=66°,
∴∠PAB+∠PBA+∠PAC+∠PCA=132°,
∵∠BPC+∠PBC+∠PCB=180°,
∴∠PAB+∠PBA+∠PAC+∠PCA+∠PBC+∠PCB=180°,
∴∠BPC=∠PAB+∠PBA+∠PAC+∠PCA=132°.
点评 考查了作图-应用与设计作图,本题用到的知识点为:到线段两个端点距离相等的点应在线段的垂直平分线上;线段的垂直平分线上的点到线段的两个端点的距离相等.等边对等角.


科目:初中数学 来源: 题型:解答题
 某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:
阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
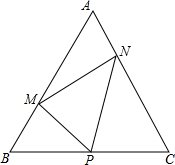 等边△ABC,P为BC中点,∠MPN=60°,求证:△BPM∽△CNP∽△PNM;MP平分∠BMN;NP平分∠CNM;MN=BM+CN-$\frac{1}{2}$AB;BM•CN=$\frac{1}{4}$AB2.
等边△ABC,P为BC中点,∠MPN=60°,求证:△BPM∽△CNP∽△PNM;MP平分∠BMN;NP平分∠CNM;MN=BM+CN-$\frac{1}{2}$AB;BM•CN=$\frac{1}{4}$AB2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,点D、E分别在边AB、AC上,且AD:DB=3:2,AE:EC=1:2,直线ED和CB的延长线交于点F,求:
在△ABC中,点D、E分别在边AB、AC上,且AD:DB=3:2,AE:EC=1:2,直线ED和CB的延长线交于点F,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC中,CD是∠ACB的角平分线.
已知,如图,△ABC中,CD是∠ACB的角平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com