
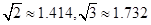 )
)
科目:初中数学 来源:不详 题型:解答题
 上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距
上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距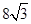 km的C处.
km的C处.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 海里,请你测算灯塔C处在观察站A的什么方向?
海里,请你测算灯塔C处在观察站A的什么方向?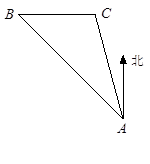
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,那么∠A 取值范围是 ( )
,那么∠A 取值范围是 ( )| A.0°< ∠A≤30° | B.30°< ∠A≤45° | C.45°<∠A ≤60° | D.60°< ∠A < 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com