Question

12．如图，在△ABC中，DE∥BC，S_△ADE：S_△ABC=9：16，求S_△ADE：S_△CDE．

Answer 1

分析 根据三角形中，DE∥BC，得到两个三角形相似，根据相似三角形的性质，相似三角形的面积之比等于对应边之比的平方，得到边AE与边BC的比值的平方，开方运算得到边长之比． 本题求两个三角形的面积之比，注意到这两个三角形是同高的三角形，所以只要看一下这两个三角形作为边的关系即可，根据在上一问中得到的AE与EC 的长度之比得到结果．

解答 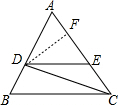解：∵DE∥BC，
∴△ADE∽△ABC． 
S_△ADE：S_△ABC=（AE：AC）²=9：16，
∴AE：AC=3：4，
∴AE：EC=3：1． 
如图，作DF⊥AC，垂足为F． 
则S△ADE=$\frac{1}{2}$DF•AE，
S△CDE=$\frac{1}{2}$DF•EC． 
∴S△ADE：S△CDE=（$\frac{1}{2}$DF•AE）：（$\frac{1}{2}$DF•EC）=AE：EC=31．

点评 本题考查了三角形相似的判定与性质，是一个证明三角形相似的题目，题目用到相似三角形的判定定理，用到相似三角形的面积，在求两个三角形面积之比的方法，是一个初中课本上出现过的问题，是一个基础题．