
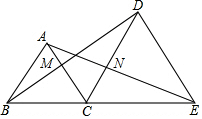
 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.分析 (2)先根据等边三角形的性质证明△ACE≌△BCD,则∠DBC=∠EAC,再证明△BCM≌△ACN(ASA),所以CM=CN,得△CMN是等边三角形,根据内错角相等得MN∥BE;
(2)画出一个反例图形即可说明.
解答 证明:(1)如图1,∵△ABC和△DCE均为等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,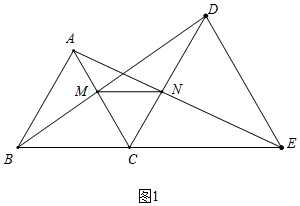
∴∠ACB+∠ACD=∠DCE+∠ACD,∠ACD=180°-60°-60°=60°,
即∠ACE=∠BCD,
在△ACE和△BCD中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴∠DBC=∠EAC,
在△BCM和△ACN中,
∵$\left\{\begin{array}{l}{∠DBC=∠EAC}\\{BC=AC}\\{∠ACB=∠ACN=60°}\end{array}\right.$,
∴△BCM≌△ACN(ASA),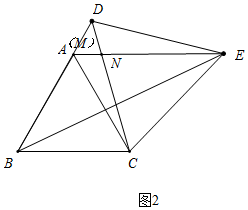
∴CM=CN,
∵∠MCN=60°,
∴△CMN是等边三角形,
∴∠CMN=60°,
∴∠CMN=∠ACB=60°,
∴MN∥BE;
(2)不成立.请看图2.当M与A重合时,显然NM与BE相交,不平行.
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会利用反例图形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
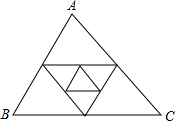 如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2016}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
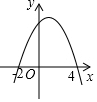 如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )| A. | x<-2 | B. | x>4 | C. | -2<x<4 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
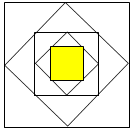 如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com