
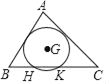
【题目】点G为△ABC的重心(△ABC三条中线的交点),以点G为圆心作⊙G与边AB,AC相切,与边BC相交于点H,K,若AB=4,BC=6,则HK的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据切线的性质得到EG⊥AB,FG⊥AC,连接AG并延长交BC于S,根据重心的性质得到BS=CS=![]() BC=3,延长AS到O时SO=AS,根据全等三角形的性质得到∠O=∠CAS,AC=OB,由勾股定理得到AS=
BC=3,延长AS到O时SO=AS,根据全等三角形的性质得到∠O=∠CAS,AC=OB,由勾股定理得到AS=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
设⊙G与边AB,AC相切于E,F,连接EG,FG,
则EG⊥AB,FG⊥AC,
连接AG并延长交BC于S,
∵EG=FG,
∴∠BAS=∠CAS,
∵点G为△ABC的重心,
∴BS=CS=![]() BC=3,
BC=3,
延长AS到O时SO=AS,
在△ACS与△OBS中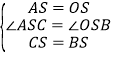 ,
,
∴△ACS≌△OBS(SAS),
∴∠O=∠CAS,AC=OB,
∵∠BAS=∠CAS,
∴∠BAS=∠O,
∴AB=BO,
∴AB=AC,
∴AS⊥BC,
∴AS=![]() ,
,
∴AG=![]() AS=
AS=![]() ,SG=
,SG=![]() AS=
AS=![]() ,
,
∵∠EAG=∠SAB,∠AEG=∠ASB=90°,
∴△AEG∽△ASB,
∴![]() ,
,
∴![]() ,
,
∴EG=![]() ,
,
连接GH,
∴GH=![]() ,
,
∴HS=![]() ,
,
∴HK=2HS=![]() .
.
故选:A.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,抛物线y=﹣![]() x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求直线BD的解析式;
(2)如图②,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() GE的值最小,求出点G的坐标及PG﹣
GE的值最小,求出点G的坐标及PG﹣![]() GE的最小值;
GE的最小值;
(3)将抛物线沿直线AC平移,点A,C平移后的对应点为A′,C'.在平面内有一动点H,当以点B,A',C',H为顶点的四边形为平行四边形时,在直线AC上方找一个满足条件的点H,与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时,求出点A′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
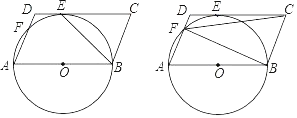
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD切于点E,AD交⊙O于点F.
(1)求证:∠ABE=45°;
(2)连接CF,若CE=2DE,求tan∠DFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
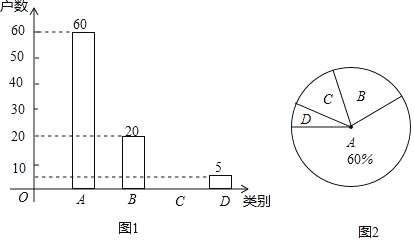
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①![]() ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
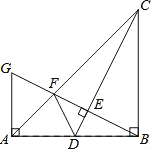
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
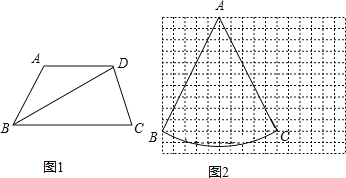
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com