
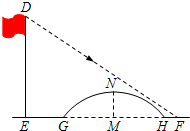
 如图所示,数学小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得小桥拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为( )
如图所示,数学小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得小桥拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为( )| A. | $\frac{5}{2}$ | B. | 5 | C. | 3$\sqrt{3}$ | D. | 6 |
分析 小桥所在圆的圆心为点O,连结OG,设⊙O的半径为r米.先利用平行投影的性质和相似的性质得到$\frac{DE}{EF}$=$\frac{1.6}{2.4}$,于是可求出GH=8米,再根据垂径定理得到点O在直线MN上,GM=HM=$\frac{1}{2}$GH=4米,然后根据勾股定理得到r2=(r-2)2+16,再解方程即可.
解答 解:如图,设小桥的圆心为O,连接OM、OG.设小桥所在圆的半径为r米.
∵$\frac{DE}{EF}$=$\frac{1.6}{2.4}$,
∴$\frac{8}{EF}$=$\frac{1.6}{2.4}$,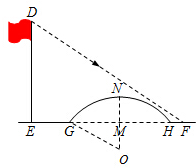 解得EF=12,
解得EF=12,
∴GH=12-3-1=8(米).
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=$\frac{1}{2}$GH=4米.
在Rt△OGM中,由勾股定理得:
OG2=OM2+GM2,
即r2=(r-2)2+16,
解得:r=5.
答:小桥所在圆的半径为5米.
故选B.
点评 此题主要考查了相似三角形的应用,勾股定理以及垂径定理的应用,根据已知得出关于r的等式是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
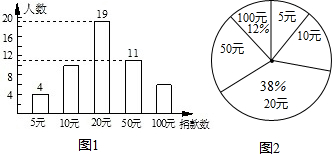
| A. | 30元 | B. | 33元 | C. | 36元 | D. | 35元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12,3 | B. | 13,3 | C. | 14,2 | D. | 13,2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com