
| A. | 25 | B. | 24 | C. | 12 | D. | 7 |
分析 根据菱形的性质得出边长AB=5,AC⊥BD,设OA=4x,OB=3x,根据勾股定理求出AB=5x,即可求出AC、BD,得出面积=$\frac{1}{2}$AC•BD.
解答 解:如图所示: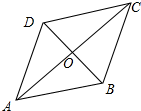
∵四边形ABCD是菱形,周长是20,
∴AB=BC=CD=DA=5,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC⊥BD,
设OA=4x,OB=3x,
则AC=8x,BD=6x,AB=$\sqrt{(4x)^{2}+(3x)^{2}}$=5x,
∴5x=5,
∴x=1,
∴AC=8,BD=6,
∴菱形ABCD的面积为:$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×8×6=24;
故选:B.
点评 本题考查了菱形的性质以及勾股定理和面积的求法;根据勾股定理求出对角线的长是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 有两边和一角对应相等的两个三角形全等 | |
| B. | 有三个角对应相等的两个三角形全等 | |
| C. | 有一边和两角对应相等的两个三角形全等 | |
| D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
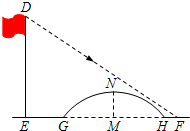 如图所示,数学小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得小桥拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为( )
如图所示,数学小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得小桥拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为( )| A. | $\frac{5}{2}$ | B. | 5 | C. | 3$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12% | B. | 30% | C. | 10% | D. | 22% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com