
科目:初中数学 来源:2014-2015学年浙江省江山市九年级上学期质量检测数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在四边形ABCD中,AD∥BC, AB=AC,BE=CE=AD.

(1)求证:四边形ECDA是矩形;
(2)当△ABC是什么类型的三角形时,四边形ECDA是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省蒙自市九年级下学期中考一模数学试卷(解析版) 题型:解答题
(9分)如图(1),在平面直角坐标系 中,抛物线
中,抛物线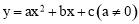 与
与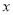 轴交于
轴交于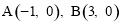 ,与y轴交于
,与y轴交于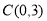 ,顶点为
,顶点为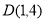 ,对称轴为
,对称轴为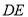 .
.
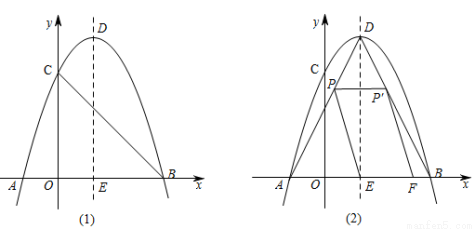
(1)抛物线的解析式是 ;
(2)如图(2),点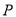 是
是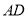 上的一个动点,
上的一个动点,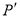 是
是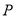 关于
关于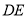 的对称点,连结
的对称点,连结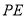 ,过
,过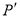 作
作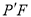 ∥
∥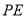 交
交 轴于
轴于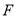 .设
.设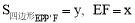 ,求
,求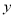 关于
关于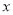 的函数关系式,并求
的函数关系式,并求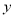 的最大值;
的最大值;
(3)在(1)中的抛物线上是否存在点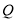 ,使
,使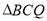 成为以
成为以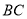 为直角边的直角三角形?若存在,求出
为直角边的直角三角形?若存在,求出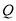 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省蒙自市九年级下学期中考一模数学试卷(解析版) 题型:选择题
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
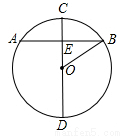
A.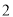 B.
B.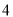 C.
C.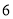 D.
D.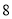
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:解答题
(12分)已知抛物线y=-x2-2x+a(a≠0)与y轴交于A,顶点为M,直线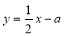 分别与x轴、y轴交于B、C两点,并且与直线MA相交于N点。
分别与x轴、y轴交于B、C两点,并且与直线MA相交于N点。
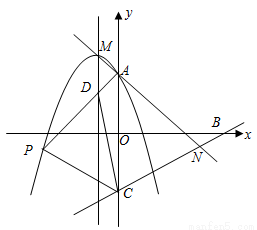
(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M、A的坐标;
(2)将△NAC沿着y轴翻折,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于D,连接CD。求a的值及△PCD的面积;
(3)在抛物线y=-x2-2x+a(a>0)上是否存在点P,使得以P、A、C、N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:填空题
下图是轰炸机群一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是 。

查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:选择题
如图,在四边形ABCD中,对角线AC、BD交于E,∠CBD=90º,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
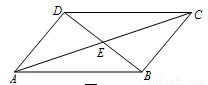
A、6 B、12 C、20 D、24
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(河南卷)数学(解析版) 题型:填空题
现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市怀柔区中考二模数学试卷(解析版) 题型:解答题
阅读理解:
学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
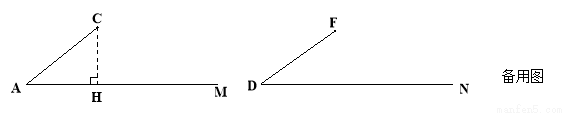
如图1,已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB<CH,CB=CH,CH<CB<CA,”三种情况进行探究.
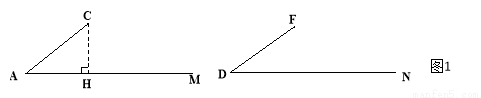
深入探究:
第一种情况,当BC<CH时,不能构成△ABC和△DEF.
第二种情况,(1)如图2,当BC=CH时,在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 ,可以知道Rt△ABC≌Rt△DEF.
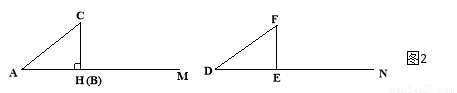
第三种情况,(2)当CH<BC<CA时,△ABC和△DEF不一定全等.请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等(表明字母,不写作法,保留作图痕迹).
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF.除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com