
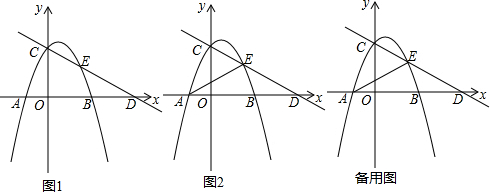
���� ��1����ȷ������C���꣬�̶��ó�OC�����ɵó�BO��AO��DO������ȷ������A��B��D�����꣬�ô���ϵ����ȷ���������߽���ʽ��
��2���������R�����꣬�����ó�ֱ��RD����ʽ���ó���M�����꣬����������ε������ʽ���ɵó�������ϵʽ��
��3����ȷ����ֱ��CD����ʽ���������߽���ʽ������õ�E�����꣬�������AE��ֱ��AE�Ľ���ʽ�������������A��ֱ��AE��ֱ�߽���ʽ�����õ���ֱ�������ε����������Q�����꣬�����ó�QE�Ľ���ʽ�����������߽���ʽ����������꣬����P�����꣮
��� �⣺��1����������y=ax2+bx+2��y�ύ�ڵ�C��
��C��0��2����
��CO=2��
��CO=2AO��
��AO=1��
��A��-1��0����
��CO=BO=BD��
��BO=2��DO=4��
��B��2��0����D��4��0����
��������y=ax2+bx+2��x�ύ�ڵ�A����B��
��$\left\{\begin{array}{l}{a-b+2=0}\\{4a+2b+2=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2+x+2��
��2����ͼ1��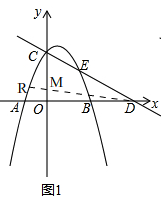
�ߵ�RΪ�������ϵڶ������ϵ�һ�㣬���R�ĺ�����t��
��R��t��-t2+t+2����
��D��4��0����
��ֱ��RD�Ľ���ʽΪy=$\frac{-{t}^{2}+t+2}{t-4}$��x-4����
��M��0��$\frac{4��{t}^{2}-t-2��}{t-4}$����
��S=$\frac{1}{2}$��2-$\frac{4��{t}^{2}-t-2��}{t-4}$��•��4-t��=2t2-3t��-1��t��0����
��3����ͼ2��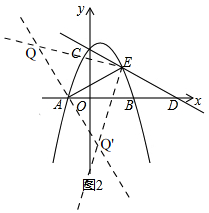
�ɣ�1��֪��C��0��2����D��4��0����
��ֱ��CD����ʽΪy=-$\frac{1}{2}$x+2�٣�
�ߵ�E��������y=-x2+x+2���ϣ�
�������٢ڵó���E��$\frac{3}{2}$��$\frac{5}{4}$����
��A��-1��0����
��AE=$\frac{5\sqrt{5}}{4}$��ֱ��AE�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{1}{2}$
����A��ֱ��QQ'��AE��
��ֱ��QQ'�Ľ���ʽΪy=-2x-2��
��Q��m��-2m-2����
��AQ=$\sqrt{5}$|m+1|��
�ߡ�PAE=45�㣬
��AE=AQ��
��$\sqrt{5}$|m+1|=$\frac{5\sqrt{5}}{4}$��
��m=$\frac{1}{4}$��m=-$\frac{9}{4}$��
�ٵ�m=$\frac{1}{4}$ʱ��Q'��$\frac{1}{4}$��-$\frac{5}{2}$����
��E��$\frac{3}{2}$��$\frac{5}{4}$����
��ֱ��Q'E�Ľ���ʽΪy=3x-$\frac{13}{4}$�ۣ��������߽���ʽΪy=-x2+x+2�ܣ�
�����ۢܵó���P������Ϊ��-$\frac{7}{2}$��-$\frac{55}{4}$����
�ڵ�m=-$\frac{9}{4}$ʱ��Q��-$\frac{9}{4}$��$\frac{5}{2}$����ͬ�ٵķ����ó���һ����P������Ϊ��-$\frac{1}{6}$��$\frac{65}{36}$����
�������������ĵ�P������Ϊ��-$\frac{7}{2}$��-$\frac{55}{4}$����-$\frac{1}{6}$��$\frac{65}{36}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ����ȷ�������ߣ�ֱ�߽���ʽ�������ε������ʽ������ֱ�������ε����ʣ�ֱ�ߺ������ߵĽ������꣬�Ȿ��Ĺؼ����ô���ϵ����ȷ����ֱ�ߵĽ���ʽ���������ϴ����״��⣮


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ʾ��Ϊ�෴�����������ǣ�������
��ͼ����ʾ��Ϊ�෴�����������ǣ�������| A�� | ��A�͵�D | B�� | ��B�͵�C | C�� | ��A�͵�C | D�� | ��B�͵�D |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
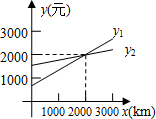 ij��˾����������ƾ��˾ǩ�����ͬ����ÿ���ó�·��x km���㣬��������ƾ��˾ÿ����ȡ������Ϊy1Ԫ����������ƾ��˾ÿ����ȡ������Ϊy2Ԫ����y1��y2��x֮��ĺ�����ϵ��ͼ��ʾ������x=0��Ӧ�ĺ���ֵΪ�¹̶����ѣ����������жϴ�����ǣ�������
ij��˾����������ƾ��˾ǩ�����ͬ����ÿ���ó�·��x km���㣬��������ƾ��˾ÿ����ȡ������Ϊy1Ԫ����������ƾ��˾ÿ����ȡ������Ϊy2Ԫ����y1��y2��x֮��ĺ�����ϵ��ͼ��ʾ������x=0��Ӧ�ĺ���ֵΪ�¹̶����ѣ����������жϴ�����ǣ�������| A�� | �����ó�·��Ϊ2000kmʱ��������������˾��������ͬ | |
| B�� | �����ó�·��Ϊ2300kmʱ����������������˾���ȽϺ��� | |
| C�� | ��ȥ�¹̶����ѣ�������˾ÿ������ȡ�ķ��ñ��ҹ�˾�� | |
| D�� | ������˾ÿ�µĹ̶����Ѹ���������˾ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{2}$�� | B�� | ��$\frac{1}{2}$��0�� | C�� | ��0��-1�� | D�� | ��-1��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-9+x2 | B�� | y=-2x+1 | C�� | y=$\sqrt{{x}^{2}+4}$ | D�� | y=-��x+1��+3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com