
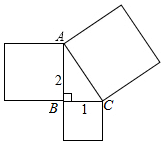
 如图,分别以Rt△ABC的边为一边向外作正方形,已知AB=2,BC=1.
如图,分别以Rt△ABC的边为一边向外作正方形,已知AB=2,BC=1.分析 (1)先根据勾股定理,求得Rt△ABC中的AC边的平方,进而得到以AC为一边的正方形的面积;
(2)根据勾股定理可得,AC的长为无理数$\sqrt{5}$,再根据$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$求得其整数部分即可.
解答 解:(1)∵Rt△ABC中,AB=2,BC=1,
∴AC2=AB2+BC2=4+1=5,
∴以AC为一边的正方形的面积为5;
(2)∵AC=$\sqrt{5}$,
∴AC的长是无理数,
又∵$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$,
∴2<$\sqrt{5}$<3,
∴$\sqrt{5}$的整数部分为2.
点评 本题主要考查了勾股定理的应用以及无理数的定义,解决问题的关键是掌握:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.解题时注意:无限不循环小数叫做无理数.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
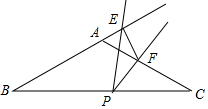 如图,在等腰△ABC中,AB=AC=8,∠BAC=120°,P为BC的中点,小慧把含30°角的透明三角板的30°角的顶点放在点P,绕P点旋转,三角板的两边分别交BA的延长线和边AC于点E、F.
如图,在等腰△ABC中,AB=AC=8,∠BAC=120°,P为BC的中点,小慧把含30°角的透明三角板的30°角的顶点放在点P,绕P点旋转,三角板的两边分别交BA的延长线和边AC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③DE=DP;④∠AOB=60°.恒成立的结论有几个( )
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③DE=DP;④∠AOB=60°.恒成立的结论有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com