

���� ��1����ͼ��֪���ص��ҵؾ���900km����ʱ3Сʱ���ɵ��г��ٶȣ��ҵ�����ؾ���150km�������õ��ס�����ľ��룻
��2��������г�������ص�ʱ�䣬Ȼ���ô���ϵ�����ֱ�����Ӽ��ҡ����ҵ���ʱ��y��x�ĺ�����ϵʽ��
��3���������������δ���ҵ�ʱ�����ҵص�·�̲�����100ǧ�ף����ѹ��ҵأ����ҵص�·�̲�����100ǧ�ף��ֱ��г�����ʽ���x�ķ�Χ���ɣ�
��� �⣺��1���ɺ���ͼ���֪����x=0ʱy=900�����ճ���ʱ�������ҵľ���Ϊ900ǧ�ף�
��x=3ʱy=0����ʾ3Сʱ���г������ҵأ�
���г��ٶ�Ϊ��900��3=300ǧ��/Сʱ��
��150��300=0.5Сʱ��
��0.5Сʱ���г�������أ��������ľ���Ϊ150ǧ�ף�
��ס������ؼ��·��Ϊ1050ǧ�ף��Ӽص����ع���3.5Сʱ��
�ʴ�Ϊ��1050��3.5��
��2����0��x��3ʱ���躯����ϵʽΪ��y=k1x+b1��
����0��900������3��0������ã�
$\left\{\begin{array}{l}{{b}_{1}=900}\\{3{k}_{1}+{b}_{1}=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{k}_{1}=-300}\\{{b}_{1}=900}\end{array}\right.$��
��y=-300x+900��
��3��x��3.5ʱ���躯����ϵʽΪ��y=k2x+b2��
����3��0������3.5��150������ã�
$\left\{\begin{array}{l}{3{k}_{2}+{b}_{2}=0}\\{3.5{k}_{2}+{b}_{2}=150}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{k}_{2}=300}\\{{b}_{2}=-900}\end{array}\right.$��
��y=300x-900��
���ϣ���0��x��3ʱ��y=-300x+900��
��3��x��3.5ʱ��y=300x-900��
��3���ٵ��г��Ӽ��ҵص�·�̲�����100ǧ��ʱ������0��x��3ʱ��
�У�-300x+900��100����ã�$\frac{8}{3}$��x��3��
�ڵ��г�������ʻ���������ҵص�·�̲�����100ǧ��ʱ������3��x��3.5ʱ��
�У�300x-900��100����ã�3��x��$\frac{10}{3}$��
���ϣ���$\frac{8}{3}$��x��$\frac{10}{3}$ʱ�������г����ҵص�·�̲�����100ǧ�ף�
���� ���⿼����һ�κ�����Ӧ�ã��������Ĺؼ��Ƕ���ͼ��ȡ�����Ϣ���ô���ϵ������������ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
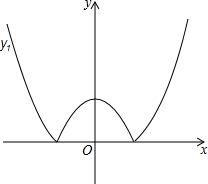 ��ͼ�������κ���y=x2-m������m��0����ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�γ��µ�ͼ���Ϊy1������һ�κ���y=x+b��ͼ���Ϊy2��������˵����
��ͼ�������κ���y=x2-m������m��0����ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�γ��µ�ͼ���Ϊy1������һ�κ���y=x+b��ͼ���Ϊy2��������˵�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
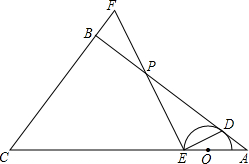 ��ͼ���ڡ�ABC�У���ABC=90�㣬AB=4��BC=3��O�DZ�AC�ϵ�һ�����㣬�Ե�OΪԲ������Բ�����AB�����ڵ�D�����߶�OC�ڵ�E������ED������E��ED�ĸߣ�������AB�ڵ�P��������CB�ڵ�F��
��ͼ���ڡ�ABC�У���ABC=90�㣬AB=4��BC=3��O�DZ�AC�ϵ�һ�����㣬�Ե�OΪԲ������Բ�����AB�����ڵ�D�����߶�OC�ڵ�E������ED������E��ED�ĸߣ�������AB�ڵ�P��������CB�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ��������ı�����ijЩ���������չ��ͼ��ͼ��������������롰�ǡ�����Ե������Σ�
��һ��������ı�����ijЩ���������չ��ͼ��ͼ��������������롰�ǡ�����Ե������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com