
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8![]() B. 8 C. 4
B. 8 C. 4![]() D. 6
D. 6
【答案】D
【解析】分析: 连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.
详解: 如图,连接OB,
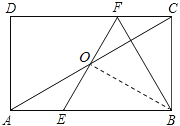
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∴∠FCA=30°,
∴∠FBC=30°,
∵FC=2,
∴BC=2![]() ,
,
∴AC=2BC=4![]() ,
,
∴AB=![]() =
=![]() =6,
=6,
故选:D.
点睛: 本题考查了矩形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形30°角所对的直角边等于斜边的一半,综合题,但难度不大,(2)作辅助线并求出∠BAC=30°是解题的关键.


科目:初中数学 来源: 题型:
【题目】为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否一定成立?说出你的理由;
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
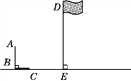
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
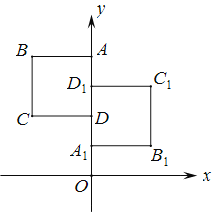
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com