
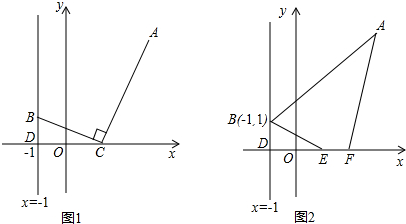
���� ���������������ε��ж�����֤�����BCD�ס�CAE���������������ε����ʵõ�����ʽ�����y��x֮��ĺ�����ϵʽ��
�����ݶ��κ���������������ֵ��
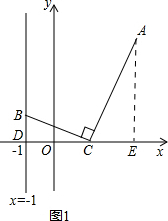
������A��x���ƽ���ߣ�������ƽ������ȡ�߶�AA��=1������B����x��ĶԳƵ�B�䣬����A��B�佻x���ڵ�E����x����ȡEF=1����ʱ�ı���ABEF���ܳ���С�����ֱ��A��B��Ľ���ʽ���Լ�����x��Ľ��㣬�õ���E�����꣮
���  �⣺������ͼ1����AE��x����E���֡�BC��AC��
�⣺������ͼ1����AE��x����E���֡�BC��AC��
���BCD+��ACE=90�㣬��A+��ACE=90�㣬
���BCD=��A���֡�CDB=��CEA=90�㣬
���BCD�ס�CAE��
��$\frac{BD}{CE}$=$\frac{CD}{AE}$��
��A��������3��4����B��������-1��y����C��������x��0����
��$\frac{y}{3-x}$=$\frac{x+1}{4}$��
��y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{3}{4}$��-1��x��3����
����y=-$\frac{1}{4}$��x-1��2+1���൱x=1ʱ��y�����ֵ1��
������ͼ2������A��x���ƽ���ߣ�������ƽ������ȡ�߶�AA��=1��
����B����x��ĶԳƵ�B�䣬����A��B�佻x���ڵ�E����x����ȡEF=1��
��ʱ�ı���ABEF���ܳ���С��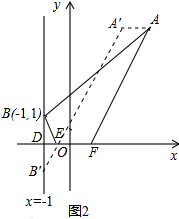
�ߵ�A������Ϊ��3��4������A�������Ϊ��2��4����
�ߵ�B������Ϊ��-1��1�������B�������Ϊ��-1��-1����
��ֱ��A��B��Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{2k+b=4}\\{-k+b=-1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{b=\frac{2}{3}}\end{array}\right.$��
ֱ��y=$\frac{5}{3}$x+$\frac{2}{3}$��x��Ľ���E������Ϊ��-$\frac{2}{5}$��0����
���߶�EFƽ�Ƶ���ͼ2��ʾ��λ��ʱ���ı���ABEF���ܳ���С��
��ʱ��E������Ϊ��-$\frac{2}{5}$��0����
���� ���⿼�����һ�κ�����֪ʶ�����κ�����֪ʶ�����������ε��ж������ʣ����ն��κ������ֵ��������ϵ������һ�κ�������ʽ�����������ε��ж��������ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
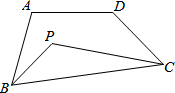 ��ͼ�����ı���ABCD�С�A+��D=m�㣬��ABC��ƽ�������BCD��ƽ���߽��ڡ�P�����PΪ$\frac{1}{2}$m�㣮
��ͼ�����ı���ABCD�С�A+��D=m�㣬��ABC��ƽ�������BCD��ƽ���߽��ڡ�P�����PΪ$\frac{1}{2}$m�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2008 | B�� | 2008 | C�� | -1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
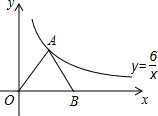 ��ͼ����A��˫����y=$\frac{6}{x}$�ϣ�BΪx����������һ�㣬����OA��AB��AO=AB�����AOB�������6��
��ͼ����A��˫����y=$\frac{6}{x}$�ϣ�BΪx����������һ�㣬����OA��AB��AO=AB�����AOB�������6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com