
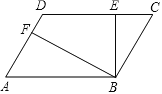
【题目】平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,若CE=2,DF=1,∠EBF=60°,求平行四边形ABCD的面积.
【答案】![]() .
.
【解析】
根据四边形的内角和等于360°,求出∠D=120°,根据平行四边形的性质得到∠A=∠C=60°,进一步求出∠ABF=∠EBC=30°,根据CE=2,DF=1,求出BC、AB的长,根据勾股定理求出BE的长,根据平行四边形的面积公式即可求出答案.
∵BE⊥CD,BF⊥AD,
∴∠BEC=∠BFD=90°,
∵∠EBF=60°,∠D+∠BED+∠BFD+∠EBF=360°,
∴∠D=120°,
∵平行四边形ABCD,
∴DC∥AB,AD∥BC,∠A=∠C,
∴∠A=∠C=180°-120°=60°,
∴∠ABF=∠EBC=30°,
∴AD=BC=2EC=4
在△BEC中由勾股定理得:BE=![]() ,
,
在△ABF中AF=4-1=3,
∵∠ABF=30,
∴AB=6,
∴平行四边形ABCD的面积是ABBE=![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
(1)(I)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为![]() ,且点B在格点上; (II)以上题中所画线段AB为一边,另外两条边长分别是3,2
,且点B在格点上; (II)以上题中所画线段AB为一边,另外两条边长分别是3,2![]() ,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
(2)所画的三角形ABC的AB边上高线长.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
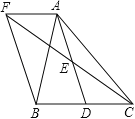
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.
(1)设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
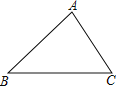
【题目】尺规作图是理论上接近完美的作图方式,乐乐很喜欢用尺规画出要求的图形.在下面的![]() 中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.
中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.
(1)作出![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ;
;
(2)作出![]() 边上的垂直平分线
边上的垂直平分线![]() 交
交![]() 于点
于点![]() ;
;
(3)连接![]() ,若
,若![]() ,则
,则![]() 的度数为 .
的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:


(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
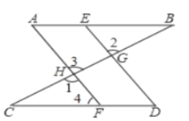
【题目】已知:如图,点![]() 分别是
分别是![]() 上的点,
上的点,![]() 分别交
分别交![]() 于
于![]() ,试说明
,试说明![]() .阅读下面的解题过程,在横线上补全推理过程或依据.
.阅读下面的解题过程,在横线上补全推理过程或依据.
解:![]() (已知)
(已知)
![]() (______________________)
(______________________)
![]() (等量代换)
(等量代换)
![]() (_____________________)
(_____________________)
∴![]() (__________________________)
(__________________________)
又![]() (已知)
(已知)
![]() (等量代换)
(等量代换)
![]() ______(____________________________)
______(____________________________)
![]() (_________________________)
(_________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
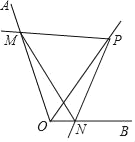
【题目】如图,点P为定角∠AOB的平分线上的一个定点,点M,N分别在射线OA,OB上(都不与点O重合),且∠MPN与∠AOB互补.若∠MPN绕着点P转动,那么以下四个结论:①PM=PN恒成立;②MN的长不变;③OM+ON的值不变;④四边形PMON的面积不变.其中正确的为_____.(填番号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com