
����Ŀ����ͼ1����֪��BAD����BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90������MΪDE���е㣮����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻
��2����ͼ1����BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2������֤����CANΪ����ֱ�������Σ�
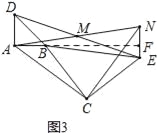
��3����ͼ1����BCE�Ƶ�B��ת��ͼ3��λ��ʱ��(2)�еĽ����Ƿ���Ȼ����������������֤��֮��������������˵�����ɣ�

���𰸡���1��֤������������2��֤������������3����ACN��Ϊ����ֱ�������Σ�֤����������
�������������������1����EN��AD�͵�MΪDE���е����֤����ADM�ա�NEM���Ӷ�֤��MΪAN���е㣮
��2����֤AB=DA=NE����ABC=��NEC=135�����Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90����������ACNΪ����ֱ�������Σ�
��3���ӳ�AB��NE�ڵ�F������ADM�ա�NEM�������ı���BCEF�ڽǺͣ��ɵ���ABC=��FEC���Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90����������ACNΪ����ֱ�������Σ�
�����������1����ͼ1��
��EN��AD��
���MAD=��MNE����ADM=��NEM��
����MΪDE���е㣬
��DM=EM��
����ADM����NEM��
��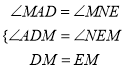 ��
��
���ADM�ա�NEM��
��AM=MN��
��MΪAN���е㣮
��2����ͼ2��
�ߡ�BAD����BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45����
��AD��NE��
���DAE+��NEA=180����
�ߡ�DAE=90����
���NEA=90����
���NEC=135����
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135����
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
����ABC����NEC��
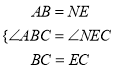
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90����
���ACNΪ����ֱ�������Σ�
��3����ACN��Ϊ����ֱ�������Σ�
֤������ͼ3���ӳ�AB��NE�ڵ�F��
��AD��NE��MΪ�е㣬
������ADM�ա�NEM��
��AD=NE��
��AD=AB��
��AB=NE��
��AD��NE��
��AF��NE��
���ı���BCEF�У�
�ߡ�BCE=��BFE=90��
���FBC+��FEC=360�㩁180��=180��
�ߡ�FBC+��ABC=180��
���ABC=��FEC
����ABC����NEC��
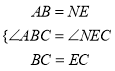
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90����
���ACNΪ����ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��F��G��H�ֱ�Ϊ����ABCD�ıߵ��е㣬AB=6cm����ABC=60�������ı���EFGH�����Ϊ__cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������E��AD�ϵ�һ�㣬��DBC=��BED.
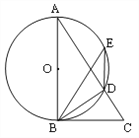
��1����֤��BC�ǡ�O�����ߣ�
��2����֪AD=3��CD=2����BC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ������ ��
A. x��2x=��x B. 2x��y=xy C. x2+x2=x4 D. 5y��3y=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ6m3��2m2+4m+2��ȥ3��2m3+m2+3m��1�����ټ�ȥ3��2m3+m2+3m��1����mΪ�������IJ�һ���ǣ� ��
A.5�ı���
B.ż��
C.3�ı���
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=6��BC=8��AC=10���ѡ�ABC��AP�۵���ʹ��AB��AC�غϣ���B����AC���ϵ�B�䴦�����ۺ�AP�ij����� �� 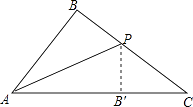
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������ε����߳��ֱ�Ϊ3��5���������ܳ�Ϊ�� ��
A. 11 B. 12 C. 13 D. 11��13
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com