
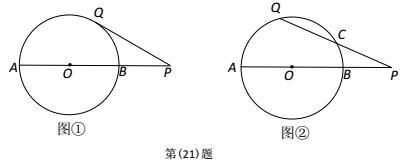
已知AB 是⊙O 的直径,点 P 在线段 AB 的延长线上,BP=OB=2,点 Q 在⊙O 上,连接 PQ.
(Ⅰ)如图①,线段 PQ 所在的直线与⊙O 相切,求线段 PQ 的长;
(Ⅱ)如图②,线段 PQ 与⊙O 还有一个公共点 C,且 PC=CQ,求线段 PQ 的长.
(Ⅰ)解:连接 QO.
∵ 线段 PQ 所在的直线与⊙O 相切,点 Q 在⊙O 上, ∴ OQ⊥QP,即∠OQP=90°.
又∵OQ= OB ,BP=OB =2,∴OQ=2,OP=4. ∴ PQ= 即线段 PQ 的长为
即线段 PQ 的长为 .
.
(Ⅱ)解:过点 O 作 OE⊥QC,垂足为 E,连接 QO.
∵ OE⊥QC,垂足为 E, ∴ QE=EC. 设 QE=x ,则 EC=x ,QC=2x.
∵PC=CQ,∴PC=2x,PE=3x,PQ=4x.
由(Ⅰ)知 OQ=2,OP=4. ∴ 在 Rt△QOE 中, OE 2= OQ 2 -QE 2 = 22-x 2 ,
在 Rt△POE 中, OE 2 = OP 2- PE 2 = 42- 9x 2 , ∴ 22- x 2 = 42-9x 2 ,
解这个方程,得  (不合题意,舍).
(不合题意,舍).
∴ PQ=4x= 4× =
= .即线段 PQ 的长为
.即线段 PQ 的长为 .
.


科目:初中数学 来源: 题型:
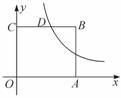
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(2,2),反比例函数y=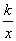 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.
(1)求k的值.
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的表达式并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数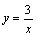 ,下列结论中,正确的是( )
,下列结论中,正确的是( )
(A)图象经过点(1,-3) (B)图象在第二、四象限
(C) x >0 时, y 随 x 的增大而增大 (D) x <0 时, y 随 x 增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com