
【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2020分钟时,这个粒子所在位置的坐标是( )
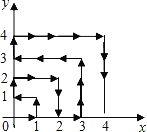
A.(4,45)B.(45,4)C.(44,4)D.(4,44)
【答案】C
【解析】
根据现有点(1,1)、(2,2)、(3,3)、(4,4)分析点的运动时间和运动方向,可以得出一般结论,然后利用这个结论算出第2020分钟时点的坐标.
粒子所在位置与运动的时间的情况如下:
位置:(1,1)运动了2=1×2分钟,方向向左,
位置:(2,2)运动了6=2×3分钟,方向向下,
位置:(3,3)运动了12=3×4分钟,方向向左,
位置:(4,4)运动了20=4×5分钟,方向向下;
…
总结规律发现,设点(n,n),
当n为奇数时,运动了n(n+1)分钟,方向向左;
当n为偶数时,运动了n(n+1)分钟,方向向下;
∵44×45=1980,45×46=2070
∴到(44,44)处,粒子运动了44×45=1980分钟,方向向下,
故到2020分钟,须由(44,44)再向下运动2020-1980=40分钟,
44-40=4,到达(44,4).
故选:C.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
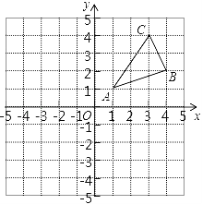
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ABC关于y轴对称的△A1B1C1;
②请画出△ABC关于x轴对称的△A2B2C2,并写出△A2B2C2各顶点坐标;
③求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
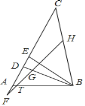
【题目】如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=![]() (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=
(∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=![]() (∠BAC﹣∠C);其中正确的是_____.
(∠BAC﹣∠C);其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题,例如:∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:(1)![]() 的整数部分是 ,小数部分是
的整数部分是 ,小数部分是
(2)∵2<![]() <3 ,∴1<4-
<3 ,∴1<4- ![]() <2,∴4-
<2,∴4- ![]() 的整数部分是1,小数部分4-
的整数部分是1,小数部分4-![]() -1=3-
-1=3-![]()
已知:9﹣![]() 小数部分是m,9+
小数部分是m,9+![]() 小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值
小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )

A. 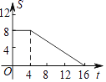 B.
B. 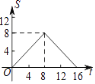 C.
C. 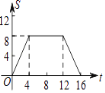 D.
D. 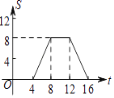
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC中,AB=AC,D、E分别是AC、AB上两点,连结BD、CE,BD=CE,且BC>BD,∠A=48°,∠BCE=36°,则∠ADB的度数等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
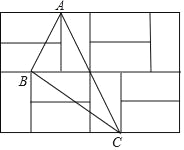
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为6,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找一格点E,使△ABE为直角三角形,求出所有满足条件的线段AE的长度.
(3)求sin∠BAC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com