
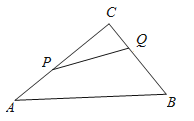
【题目】如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.
(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
(3)是否存在某一时刻,PQ长为![]() ,如果存在,求出运动时间t。
,如果存在,求出运动时间t。
【答案】(1)1或3秒;(2)不存在满足条件的t;(3)![]()
【解析】
(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)将△PBQ的面积表示出来,根据△=b2-4ac来判断;
(3)设经过y秒后存在,则PC=8-2y,CQ=y,根据勾股定理可得PC2+CQ2=(![]() )2,求方程即可.
)2,求方程即可.
(1)解:设经过x秒,△CPQ的面积等于3cm2.则
![]() x(8﹣2x)=3,
x(8﹣2x)=3,
化简得x2﹣4x+3=0,
解得x1=1,x2=3;
(2)设存在某一时刻t,使PQ恰好平分△ABC的面积.则
![]() t(8﹣2t)=
t(8﹣2t)=![]() ×
×![]() ×6×8,
×6×8,
化简得t2﹣4t+12=0,
b2﹣4ac=16﹣48=﹣32<0,
故方程无实数根,即不存在满足条件的t.
(3)设经过y秒后存在PQ长为![]() ,则PC=8-2y,CQ=y,
,则PC=8-2y,CQ=y,
∵∠C=90°,
∴PC2+CQ2=(![]() )2,
)2,
解得:y1=![]() ,y2=5(不符合题意,舍去),
,y2=5(不符合题意,舍去),
所以经过![]() 秒后,PQ的长为
秒后,PQ的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列两个三角形不一定相似的是
A.两条直角边的比都是![]() 的两个直角三角形
的两个直角三角形
B.腰与底的比都是![]() 的两个等腰三角形
的两个等腰三角形
C.有一个内角为![]() 的两个直角三角形
的两个直角三角形
D.有一个内角为![]() 的两个等腰三角形
的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
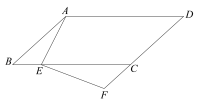
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吴京同学根据学习函数的经验,对一个新函数y=![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整
的图象和性质进行了如下探究,请帮他把探究过程补充完整
(1)该函数的自变量x的取值范围是 .
(2)列表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … |
| m | ﹣1 |
| ﹣5 | n | ﹣1 |
|
| … |
表中m= ,n= .
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系xOy中,描出上表中各对对值为坐标的点(其中x为横坐标,y为纵坐标),并根据描出的点画出该函数的图象:
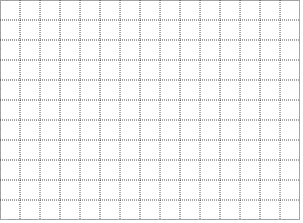
(4)观察所画出的函数图象,写出该函数的两条性质:
① ;
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
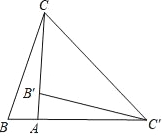
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对70周年国庆阅兵仪式直播的收看情况,某校对部分学生进行了一次调査,调査直播收看情况分三种:A.全程收看直播;B.观看了一部分直播;C.没有观看.学校学生会将调査数据进行了整理,并绘制了如下两幅不完整的统计图,请根据相关信息,解答下列问题:
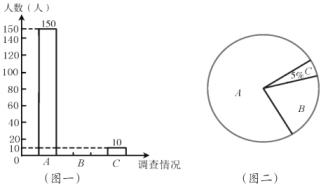
(1)本次活动共调查了______名学生;
(2)图二中![]() 区域的圆心角的度数为______;
区域的圆心角的度数为______;
(3)补全图;
(4)若该校学生共有3000名,请估计该校学生全程收看直播的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com