
分析 (1)移项后两边开方,即可得出两个一元一次方程,求出方程的解即可;
(2)把常数项1移项后,应该在左右两边同时加上一次项系数-5的一半的平方;
(3)利用配方法解方程;
(4)设t=x-2,原方程转化为9t2-6t+1=0,通过解该方程求得t的值;然后代入来求x的值.
解答 解:(1)(x-5)2-9=0,
(x-5)2=9,
x-5=±3,
x1=8,x2=2;
(2)x2-5x+1=0,
x2-5x=-1
x2-5x+$\frac{25}{4}$=-1+$\frac{25}{4}$,
(x-$\frac{5}{2}$)2=$\frac{21}{4}$
x1=$\frac{5+\sqrt{21}}{2}$,x2=$\frac{5-\sqrt{21}}{2}$;
(3)3y2-1=6y,
y2-2y+1=$\frac{1}{3}$+1,
(y-1)2=$\frac{4}{3}$,
y-1=±$\frac{2\sqrt{3}}{3}$,
y1=$\frac{3+2\sqrt{3}}{3}$,y2=$\frac{3-2\sqrt{3}}{3}$;
(4)设t=x-2,原方程转化为9t2-6t+1=0,
整理,得
(3t-1)2=0,
解得t=$\frac{1}{3}$,
所以x-2=$\frac{1}{3}$,
则x1=x2=$\frac{7}{3}$.
点评 本题考查了解一元二次方程的应用,主要考查学生的计算能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
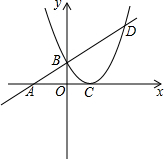 如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次图象交于y轴上的一点B,二次函数的顶点C在x轴上,且OC=2.
如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次图象交于y轴上的一点B,二次函数的顶点C在x轴上,且OC=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是多少?
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
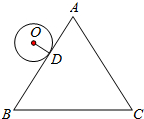 如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )| A. | 3周 | B. | 4周 | C. | 5周 | D. | 6周 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com