
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5, 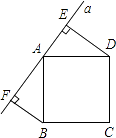
(1)求EF的长.
(2)求正方形ABCD的面积.
【答案】
(1)解:∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴D作BF⊥a于点F,DE⊥a于点E,
∴∠DEA=∠AFB=90°,
∴∠EDA+∠AED=90°,∠EAD+∠FAB=90°,
∴∠EDA=∠FAB,
在△AED和△BFA中
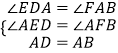
∴△AED≌△BFA(AAS),
∴AE=BF,AF=DE,
∵DE=8,BF=5,
∴AE=5,AF=8,
∴EF=AE+AF=8
(2)解:在Rt△AFB中,由勾股定理得:AB2=AF2+BF2=82+52=89,
即正方形ABCD的面积为89
【解析】(1)根据正方形的性质得出AD=AB,∠BAD=90°,根据垂直得出∠DEA=∠AFB=90°,求出∠EDA=∠FAB,根据AAS推出△AED≌△BFA,根据全等三角形的性质得出AE=BF=5,AF=DE=8,即可求出答案;(2)根据勾股定理求出AB2=AF2+BF2=89,即可得出答案.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=110厘米,∠BAC=37°,垂直支架CD=57厘米,DE是另一根辅助支架,且∠CED=60°.
(1)求辅助支架DE长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果精确到1厘米,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)a24÷[(a2) 3) 4;
(2)( a3·a4) 2÷(a3) 2÷a;
(3)- x12÷(-x4) 3;
(4)( x6÷x4·x2) 2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[ ![]() +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“全国文明村”白村果农王保收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王保如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王保应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 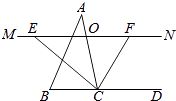
(1)求证:EO=FO;
(2)当CE=12,CF=10时,求CO的长;
(3)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F. 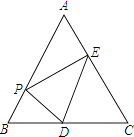
(1)求∠APE的度数;
(2)连接DE,当△PDE为等边三角形时,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com