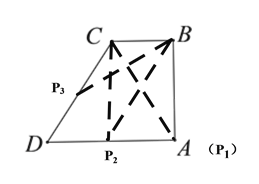
【题目】已知：如图，在四边形中ABCD中，AB⊥BC，AD∥BC，∠BCD=120°，BC=2，AD=DC.P为四边形ABCD边上的任意一点，当∠BPC=30°时，CP的长为______．
【答案】2或2
或4
【解析】过点C作CE⊥AD， 连接AC，∵AD//BC，∠BCD=120°，∴∠D=180°-∠BCD=60°，∵AD=CD，∴△ACD是等边三角形，∴∠CAD=60°，AC=AD，∵∠BAD=90°，∴∠BAC=30°，即点P1与点A重合时，∠BP1C=30°，此时CP1=CA=4；
当点P2为AD中点时，此时四边形ABCP2是矩形，∴BP2=AC=4，∠BP2C=∠BCA=30°，∵∠BCP2=90°，∴CP2=
=
；
当点P3的CD边上时，∵∠BCD=120°，∠BCP3=30°，∴∠CBP3=30°，∴CP3=BC=2；
综上，当∠BPC=30°时，CP的长为4或
或2.
黎明文化寒假作业系列答案科目：初中数学 来源： 题型：
【题目】已知点A（2，a）在抛物线y=x2上
（1）求A点的坐标；
（2）在x轴上是否存在点P，使△OAP是等腰三角形？若存在写出P点坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点M（﹣3，2）关于y轴对称的点的坐标为（ ）
A. （3，2） B. （3，﹣2） C. （﹣3，﹣2） D. （﹣3，2）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】据报道，2016年初我国网民规模达719 000 000人，将这个数用科学记数法表示为（ ）
A.7.19×109
B.7.19×108
C.71.9×107
D.0.719×109
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线：y＝ax2＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．
(1)求抛物线的解析式；
(2)T是抛物线对称轴上的一点，且△ACT是以AC为底的等腰三角形，求点T的坐标；
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行．当点M原点时，点Q立刻掉头并以每秒
个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥轴，交AC或BC于点P．求点M的运动时间t(秒)与△APQ的面积S的函数关系式，并求出S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明从家去体育场锻炼，同时，妈妈从体育场以50米/分的速度回家，小明到体育场后发现要下雨，立即返回，追上妈妈后，小明以250米/分的速度回家取伞，立即又以250米/分的速度折回接妈妈，并一同回家．如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图像．
（注：小明和妈妈始终在同一条笔直的公路上行走，图像上A、C、D三点在一条直线上）
（1）求线段BC的函数表达式；
（2）求点D坐标；
（3）当 x的值为 时，小明与妈妈相距1 500米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，4），B（2，4），C（3，﹣1）．
（1）试在平面直角坐标系中，标出A、B、C三点；
（2）求△ABC的面积．
（3）若△A1B1C1与△ABC关于x轴对称，写出A1、B1、C1的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】据统计，某小区2011年底拥有私家车125辆，2013年底私家车的拥有量达到180辆．
(1)若该小区2011年底到2014年底私家车拥有量的年平均增长率相同，则该小区到2014年底私家车将达到多少辆？
(2)为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1 000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com