
分析 设抛物线y=x2+2mx+m-7与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,因为α、β是关于x的方程x2+2mx+m-7=0的两个不相等的实数根,所以由根与系数关系得:α+β=-2m,αβ=m-7,再根据抛物线y=x2+2mx+m-7与x轴的两个交点分别位于点(1,0)的两旁可得α<1,β>1,进而可求出m的取值范围.
解答 解:∵抛物线y=x2+2mx+m-7与x轴的两个交点在(1,0)两旁,
∴关于x的方程x2+2mx+m-7=0有两个不相等的实数根,
∴△=b2-4ac>0,
即:(2m)2-4(m-7)>0,
∴m为任意实数①
设抛物线y=x2+2mx+m-7与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β
∴α、β是关于x的方程x2+2mx+m-7=0的两个不相等的实数根,
由根与系数关系得:α+β=-2m,αβ=m-7,
∵抛物线y=x2+2mx+m-7与x轴的两个交点分别位于点(1,0)的两旁
∴α<1,β>1
∴(α-1)(β-1)<0
∴αβ-(α+β)+1<0
∴(m-7)+2m+1<0
解得:m<2②
由①、②得m的取值范围是m<2,
故答案为:m<2.
点评 本题考查了抛物线与x轴的交点问题,注:当抛物线y=ax2+bx+c与轴有两个交点时,一元二次方程ax2+bx+c=0有两个不等的实数根即△>0;当抛物线y=ax2+bx+c与轴有一个交点时,一元二次方程ax2+bx+c=0有两个相等的实数根即△=0;当抛物线y=ax2+bx+c与轴无交点时,一元二次方程ax2+bx+c=0无实数根即△<0.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
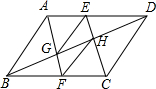 如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.
如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
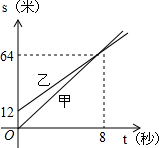 如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
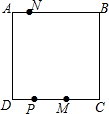 如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?
如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
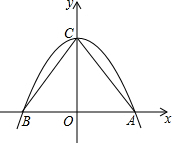 如图,抛物线y=-x2+4交x轴于A、B两点,顶点为C.
如图,抛物线y=-x2+4交x轴于A、B两点,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2044×1011 | B. | 20.44×109 | C. | 2.044×108 | D. | 2.044×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com