Question

【题目】如图，四边形是平行四边形，，，是的中点，是延长线上一点．

（1）若，求证：；

（2）在（1）的条件下，若的延长线与交于点，试判定四边形是否为平行四边形？并证明你的结论(请先补全图形，再解答)；

（3）若，与垂直吗？若垂直给出证明，若不垂直说明理由．

Answer 1

【答案】（1）证明见解析（2）四边形ACPE为平行四边形（3）垂直

【解析】

试题分析：（1）根据平行四边形的性质知道AD=AC，AD⊥AC，连接CE，根据全等三角形的判定和性质即可得到结论；

（2）根据全等三角形的性质得到CF=AD，等量代换得到AC=CF，于是得到CP=AB=AE，根据平行四边形的判定定理即可得到四边形ACPE为平行四边形；

（3）过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N，证得△AME≌△CNE，△ADE≌△CFE，根据全等三角形的性质即可得到结论．

试题解析：（1）在ABCD中，

∵AD=AC，AD⊥AC，

∴AC=BC，AC⊥BC，

连接CE，

∵E是AB的中点，

∴AE=EC，CE⊥AB，

∴∠ACE=∠BCE=45°，

∴∠ECF=∠EAD=135°，

∵ED⊥EF，

∴∠CEF=∠AED=90°﹣∠CED，

在△CEF和△AED中， ，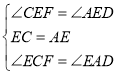

∴△CEF≌△AED，

∴ED=EF；

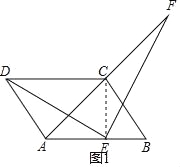
（2）由（1）知△CEF≌△AED，CF=AD，

∵AD=AC，

∴AC=CF，

∵DP∥AB，

∴FP=PB，

∴CP=AB=AE，

∴四边形ACPE为平行四边形；

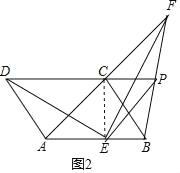
（3）垂直，

理由：过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N，

在△AME与△CNE中， ，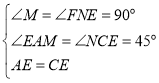

∴△AME≌△CNE，

∴∠ADE=∠CFE，

在△ADE与△CFE中， ，

∴△ADE≌△CFE，

∴∠DEA=∠FEC，

∵∠DEA+∠DEC=90°，

∴∠CEF+∠DEC=90°，

∴∠DEF=90°，

∴ED⊥EF．