
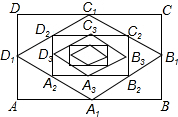
 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n. 分析 ①根据题意求出菱形ABCD的周长,根据中点四边形的性质得到A8B8C8D8是菱形,根据题意总结规律得到答案;
②根据中点四边形的面积等于原四边形面积的一半即可解决问题;
解答 解:根据中点四边形的性质可知,A1B1C1D1、A3B3C3D3…是矩形,
A2B2C2D2、A4B4C4D4…是菱形,
∵菱形ABCD的周长是(16+12)×2=56,
∴菱形A2B2C2D2的周长是56×$\frac{1}{2}$,
菱形A4B4C4D4的周长是56×$\frac{1}{{2}^{2}}$,
…
则四边形A8B8C8D8的周长是56×$\frac{1}{{2}^{4}}$=4.
易知四边形A1B1C1D1的面积=$\frac{1}{2}$•S矩形ABCD,
四边形A2B2C2D2的面积=$\frac{1}{2}$×四边形A1B1C1D1的面积=($\frac{1}{2}$)2•S矩形ABCD,
四边形A3B3C3D3的面积=($\frac{1}{2}$)3•S矩形ABCD,
…,
∴四边形AnBnCnDn的面积=($\frac{1}{2}$)n••S矩形ABCD=192•($\frac{1}{2}$)n,
故答案为4,192×($\frac{1}{2}$)n.
点评 本题考查矩形的性质、菱形的判定和性质,中点四边形等知识,解题的关键是学会从特殊到一般的探究方法,利用规律解决问题,记住中点四边形的面积等于原四边形面积的一半,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
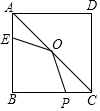 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 在数学课上,老师提出如下问题: 已知:Rt△ABC,∠ABC=90° 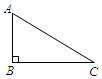 求作:矩形ABCD. |
①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 汽车行驶时间t(小时) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(升) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com