练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    四边形ABCD中，∠A:∠B:∠C:∠D=2:1:1:2，则四边形ABCD的形状是
    A．菱形B．矩形C．等腰梯形D．平行四边形
    C
    解：如图，

    ∵∠A：∠B：∠C：∠D=2：1：1：2，∴∠A=∠D，∠B=∠C，且∠A≠∠B，∠C≠∠D，∴2（∠A+∠B）=360°，∴∠A+∠B=180°，即同旁内角互补；∴四边形ABCD的形状是等腰梯形．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，在梯形ABCD中，AD∥BC， BC＝30cm，动点M从A点开始沿AD边向D以1cm/s的速度运动，动点N从C点开始沿CB边向B以3cm/s的速度运动，M、N分别从A、C同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为t s，t为何值时，四边形ABNM是平行四边形？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，四边形ABCD中，AB="BC," ∠ABC=∠CDA=90°，BE⊥AD于点E,且四边形ABCD的面积为8，则BE=   .

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图1，过△ABC的顶点A作高AD，将点A折叠到点D（如图2），这时EF为折痕，且△BED和△CFD都是等腰三角形，再将△BED和△CFD沿它们各自的对称轴EH、FG折叠，使B、C两点都与点D重合，得到一个矩形EFGH（如图3），我们称矩形EFGH为△ABC的边BC上的折合矩形．

    （1）若△ABC的面积为6，则折合矩形EFGH的面积为        ；
    （2）如图4，已知△ABC，在图4中画出△ABC的边BC上的折合矩形EFGH；
    （3）如果△ABC的边BC上的折合矩形EFGH是正方形，且BC=2a，那么，BC边上的高AD=      ，正方形EFGH的对角线长为        ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

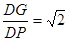    已知：如图，在正方形ABCD中，P为对角线AC上的一动点，PE⊥AB于E，PF⊥BC于F，过点P作DP的垂线交BC于点G，DG交AC于点Q.下列说法：①EF＝DP；②EF⊥DP；③；
    ④.其中正确的是
    A．①②③④B．①②③C．①②④D．①③④

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图所示，平行四边形ABCD 中∠C=108°BE平分∠ABC，则∠AEB等于    （    ）
    A．180°B．36°C．72°D．108°

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图1，在正方形中，点分别为边的中点，相交于点，则可得结论：①；②．（不需要证明）
    （1）如图2，若点不是正方形的边的中点，但满足，则上面的结论①，②是否仍然成立？（请直接回答“成立”或“不成立”）
    （2）如图3，若点分别在正方形的边的延长线和的延长线上，且，此时上面的结论1，2是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由．
    （3）如图4，在（2）的基础上，连接和，若点分别为的中点，请判断四边形是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，从下列图中选择四个拼图板，可拼成一个矩形，正确的选择方案为　①②③④　．
    （只填写拼图板的代码）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如下图，直角梯形ABCD中，AD∥BC，AD=24，BC=26，∠B=90°，动点P从A开始沿AD边向D以1的速度运动，动点Q从点C开始沿CB以3的速度向点B运动．P、Q同时出发，当其中一点到达顶点时，另一点也随之停止运动，设运动时间为，问为何值时，（1）四边形PQCD是平行四边形．（2）当为何值时，四边形PQCD为等腰梯形．

    查看答案和解析>>

    同步练习册答案