
 在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$.
在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$. 分析 作过B作BP⊥AE于P,根据勾股定理计算$BE=\frac{1}{2}$BC=2$\sqrt{5}$,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10,得B,F,G共线,作辅助线,构建直角三角形,利用同角的三角函数得:FQ=$\frac{4\sqrt{5}}{5}$,BQ=$\frac{8\sqrt{5}}{5}$,分别计算FS、GS、DG、DH、AH、AN的长,利用面积差S△MNF=S△ANF-S△AMN求值.
解答  解:过B作BP⊥AE于P,
解:过B作BP⊥AE于P,
∵正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,
∴$BE=\frac{1}{2}$BC=2$\sqrt{5}$,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10,
∴BP=$\frac{AB•BE}{AE}$=$\frac{4\sqrt{5}×2\sqrt{5}}{10}$=4,
∴PE=$\sqrt{B{E}^{2}-B{P}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{4}^{2}}$=2,
∴EF=EP,
∴F与P重合,
∴B,F,G共线,
过F作OS⊥DC,交AB于O,DC于S,则OS⊥AB,
过F作FQ⊥BC于Q,
sin∠FBE=$\frac{EF}{BE}=\frac{FQ}{BF}$,
∴$\frac{2}{2\sqrt{5}}=\frac{FQ}{4}$,
∴FQ=$\frac{4\sqrt{5}}{5}$,
∴BQ=$\frac{8\sqrt{5}}{5}$,
易得矩形OFQB,
∴FO=BQ=$\frac{8\sqrt{5}}{5}$,
∴FS=4$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{12\sqrt{5}}{5}$,AO=AB-OB=4$\sqrt{5}$-$\frac{4\sqrt{5}}{5}$=$\frac{16\sqrt{5}}{5}$,
∵GF⊥AE,
∴∠AFG=90°,
∴∠GFS+∠AFH=∠AFH+∠FAH,
∴∠GFS=∠FAB,
∴tan∠FAB=tan∠GFS=$\frac{BE}{AB}=\frac{GS}{FS}$,
∴$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{GS}{\frac{12\sqrt{5}}{5}}$,
∴GS=$\frac{6\sqrt{5}}{5}$,
∴DG=DS-GS=AO-GS=$\frac{16\sqrt{5}}{5}$-$\frac{6\sqrt{5}}{5}$=2$\sqrt{5}$,
∵GH=GF,
∴DH2+DG2=GS2+FS2,
∴DH2+(2$\sqrt{5}$)2=$(\frac{6\sqrt{5}}{5})^{2}+(\frac{12\sqrt{5}}{5})^{2}$,
∴DH=4,
∴AH=4$\sqrt{5}$-4,
tan∠ANH=tan∠DHG=$\frac{AH}{AN}=\frac{DG}{DH}$,
∴$\frac{4\sqrt{5}-4}{AN}=\frac{2\sqrt{5}}{4}$,
AN=$\frac{40-8\sqrt{5}}{5}$,
过M作MR⊥AB于R,
设MR=x,则AR=2x,
tan∠ANH=tan∠DHG=$\frac{DG}{DH}=\frac{MR}{RN}$,
∴$\frac{2\sqrt{5}}{4}=\frac{x}{RN}$,
∴RN=$\frac{4x}{2\sqrt{5}}$,
由AR+RN=AN得:2x+$\frac{4x}{2\sqrt{5}}$=$\frac{40-8\sqrt{5}}{5}$,
x=6-2$\sqrt{5}$,
∴MR=6-2$\sqrt{5}$,
∴S△MNF=S△ANF-S△AMN=$\frac{1}{2}$AN•FO-$\frac{1}{2}$AN•MR=$\frac{1}{2}$AN(FO-MR)=$\frac{1}{2}$×$\frac{40-8\sqrt{5}}{5}$×($\frac{8\sqrt{5}}{5}$-6+2$\sqrt{5}$)=$\frac{96\sqrt{5}-192}{5}$.
故答案为:$\frac{96\sqrt{5}-192}{5}$.
点评 本题考查了正方形的性质、旋转的性质、三角函数、勾股定理等知识,在四边形的计算中,常运用同角的三角函数或勾股定理列式求线段的长,也可以利用证明两三角形相似求线段的长,相比较而言,利用同角的三角函数比较简单,本题计算量大,有难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
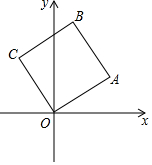 已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>2 | B. | m<2 | C. | m>-2 | D. | m<-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com