
 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.分析 (1)根据基本尺规作图作出符合条件的直线即可;
(2)过A作AF⊥BC于F,连接DA,设BE=x,根据正弦和余弦的定义用x表示出AF、AD、DF,根据勾股定理列出方程,解方程即可.
解答 解:(1)如图1所示: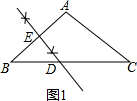
(2)过A作AF⊥BC于F,连接DA,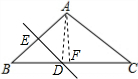
∵DE是AB的垂直平分线,
∴DA=DB,
∵在Rt△BED中,sinB=$\frac{3}{5}$,
∴cosB=$\frac{4}{5}$,
设BE=x,BD=$\frac{5}{4}$x,
则AE=BE=x,AD=BD=$\frac{5}{4}$x,
∵AB=2x,cosB=$\frac{4}{5}$,
∴AF=$\frac{6}{5}$x,BF=$\frac{8}{5}$x,
∴DF=CD-CF=13-$\frac{8}{5}$x,
在△ADF中,AD2=DF2+AF2,
即($\frac{5}{4}$x)2=(13-$\frac{8}{5}$x)2+($\frac{6}{5}$x)2,
解得,x1=10.4,x2=6.67,
△ABC的周长=AB+AC+BC=4x+$\frac{5}{4}$x+13,
当x=10.4时,△ABC的周长=67.6,
当x=6.67时,△ABC的周长=48.02.
答:△ABC的周长为48.02或67.6.
点评 本题主要考查了线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a2×2a2=6a2 | B. | (2x-1)•3x2y=6x3y-1 | ||
| C. | (-ab)3÷(-ab)=a2b2 | D. | ($\frac{1}{3}$)0×3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.
如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定是实数 | B. | 是无理数 | ||
| C. | 不存在 | D. | 当a≠0时,$\frac{1}{a}$一定是有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
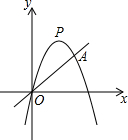 如图,二次函数y=-x2+4x与一次函数y=$\frac{1}{2}$x的图象相交于点A.
如图,二次函数y=-x2+4x与一次函数y=$\frac{1}{2}$x的图象相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com