
解分式方程: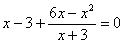 .
.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
下列结论正确的是( )
A.3a2b-a2b=2
B.单项式-x2的系数是-1
C.使式子 有意义的x 的取值范围是x>-2
有意义的x 的取值范围是x>-2
D.若分式 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
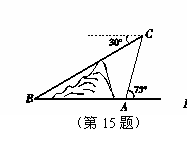
如图,在小山的东侧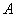 点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成
点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成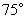 角的方向飞行,25分钟后到达
角的方向飞行,25分钟后到达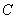 处,此时热气球上的人测得小山西侧
处,此时热气球上的人测得小山西侧 点的俯角为
点的俯角为 ,则小山东西两侧
,则小山东西两侧 ,
, 两点间的距离为 米.
两点间的距离为 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
数学活动——求重叠部分的面积.
问题情境:数学活动课上,老师出示了一个问题:
如图1,将两块全等的直角三角形纸片 和
和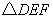 叠放在一起,其中
叠放在一起,其中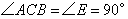 ,
, ,顶点
,顶点 与边
与边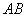 的中点重合.
的中点重合.
 (中等题)(1)若
(中等题)(1)若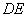 经过点
经过点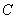 ,
,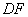 交
交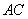 于点
于点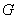 ,求重叠部分(
,求重叠部分(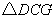 )的面积;
)的面积;
(稍难题)(2)合作交流:“希望”小组受问题(1)的启发,将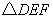 绕点
绕点 旋转,使
旋转,使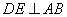 交
交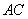 于点
于点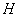 ,
,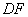 交
交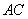 于点
于点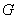 ,如图2,求重叠部分(
,如图2,求重叠部分(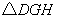 )的面积.
)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
小王参加某企业招聘测试,他的笔试,面试、技能操作得分分别为85分,80分,90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A. 255分 B. 84分 C. 84.5分 D.86分
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.
(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.
请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
 |  | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com