
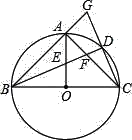
【题目】已知:如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆,BD平分∠ABC交⊙O于D,且BD与OA、AC分别交于点E、F延长BA、CD交于G.
(1)试证明:BF=CG.
(2)线段CD与BF有什么数量关系?为什么?
(3)试比较线段CD与BE的大小关系,并说明理由.
【答案】(1)见解析;(2)线段2CD=BF,理由见解析;(3)见解析.
【解析】
(1)根据圆周角定理以及全等三角形的判定得出△ABF≌△ACG即可求出答案;
(2)利用角平分线的性质以及圆周角定理得出△BDG≌△BDC,进而得出GD=CD,求出![]() ,即可得出答案;
,即可得出答案;
(3)利用等腰三角形的性质得出BE=EC,再利用直角三角形边之间大小关系求出即可.
(1)∵⊙O是以等腰三角形ABC的底边BC为直径的外接圆,
∴AB=AC,∠BAC=90°,∠ABD=∠DCA,
∴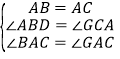 ,
,
∴△ABF≌△ACG,(AAS)
∴BF=CG;
(2)线段2CD=BF,
证明:∵BD平分∠ABC交⊙O于D,
∴∠GBD=∠CBD,
∵BC为直径,
∴∠BDC=90°,
∴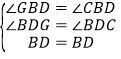 ,
,
∴△BDG≌△BDC,(AAS)
∴GD=CD,
∵BF=CG,
∴![]() ,
,
即![]() ,
,
∴2CD=BF;
(3)连接EC,
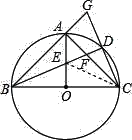
∵△ABC是等腰三角形,AB=AC,
且BO=CO,
∴AO⊥BC(等腰三角形三线合一),
∴BE=EC,
∵∠EDC=90°,在△EDC中所对斜边为EC,
∴EC>CD(直角三角形中斜边大与直角边长),
∴BE>CD.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
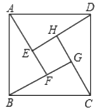
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于等腰三角形,以下说法正确的是( )
A.有一个角为40°的等腰三角形一定是锐角三角形
B.等腰三角形两边上的中线一定相等
C.两个等腰三角形中,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等
D.等腰三角形两底角的平分线的交点到三边距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
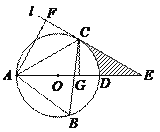
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
如图1,已知△ABC中,AD 为中线.延长AD至点E,使 DE=AD.在△ADC和△EDB中,AD=DE,∠ADC=∠EDB,BD=CD,所以,△ACD≌△EBD,进一步可得到AC=BE,AC//BE等结论.
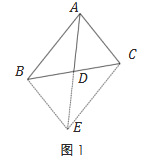
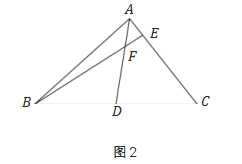
在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.
解决问题:如图2,在△ABC中,AD是三角形的中线,点F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
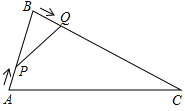
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7
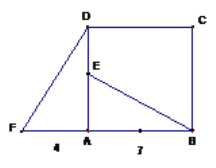
(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
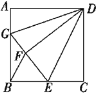
【题目】如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交
AB于G,连接DG,现在有如下4个结论:①![]() ≌
≌![]() ;②
;②![]() ;③∠GDE=45°;④
;③∠GDE=45°;④
DG=DE在以上4个结论中,正确的共有( )个
A. 1个 B. 2 个 C. 3 个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com