
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
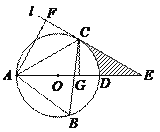
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)略
(2)![]()
【解析】
(1) 如图,连结CD,OC,则∠ADC=∠B= 60°.
∵AC⊥CD,CG⊥AD,∴∠ACG=∠ADC= 60°.
由于∠ODC= 60°,OC=OD,∴△OCD为正三角形,得∠DCO= 60°.
由OC⊥l,得∠ECD= 30°,∴∠ECG= 30° + 30° = 60°.
进而∠ACF= 180°-2×60° = 60°,∴ △ACF≌△ACG.
(2)在Rt△ACF中,∠ACF= 60°,AF= 4![]() ,得CF= 4.
,得CF= 4.
在Rt△OCG中,∠COG= 60°,CG=CF= 4,得OC=![]() .
.
在Rt△CEO中,OE=![]() .
.
于是S阴影=S△CEO-S扇形COD=![]() =
=![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
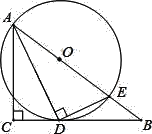
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O
(1)求证:点D在⊙O上;
(2)求证:BC是⊙O的切线;
(3)若AC=6,BC=8,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
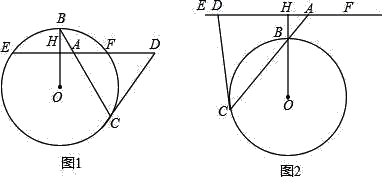
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
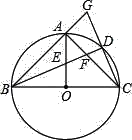
【题目】已知:如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆,BD平分∠ABC交⊙O于D,且BD与OA、AC分别交于点E、F延长BA、CD交于G.
(1)试证明:BF=CG.
(2)线段CD与BF有什么数量关系?为什么?
(3)试比较线段CD与BE的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
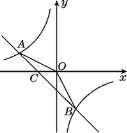
【题目】已知一次函数y=kx+b和反比例函数y=![]() 图象相交于A(-4,2),B(n,-4)两点.
图象相交于A(-4,2),B(n,-4)两点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b-![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
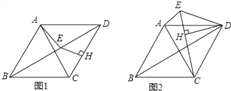
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com