
【题目】已知一次函数y=kx+b和反比例函数y=![]() 图象相交于A(-4,2),B(n,-4)两点.
图象相交于A(-4,2),B(n,-4)两点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b-![]() <0的解集.
<0的解集.
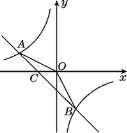
【答案】(1) y=-![]() , y=-x-2;(2)6;(3) x>2或-4<x<0.
, y=-x-2;(2)6;(3) x>2或-4<x<0.
【解析】
(1)先把点A的坐标代入反比例函数解析式,即可得到m=-8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)先求出直线y=-x-2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x>2或-4<x<0时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
(1)把A(-4,2)的坐标代入y=![]() ,得m=2×(-4)=-8,
,得m=2×(-4)=-8,
∴反比例函数的解析式为y=-![]() .
.
把B(n,-4)的坐标代入y=-![]() ,得-4n=-8,
,得-4n=-8,
解得n=2.∴B(2,-4).
把A(-4,2)和B(2,-4)的坐标代入y=kx+b,得
![]() 解得
解得![]()
∴一次函数的解析式为y=-x-2.
(2)y=-x-2中,令y=0,则x=-2,
即直线y=-x-2与x轴交于点C(-2,0).
∴S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.
(3)由图可得,不等式kx+b-![]() >0的解集为x>2或-4<x<0.
>0的解集为x>2或-4<x<0.


科目:初中数学 来源: 题型:
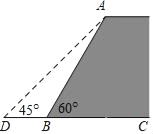
【题目】如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=45°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
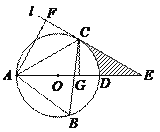
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
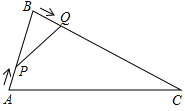
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
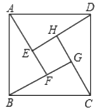
【题目】赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7
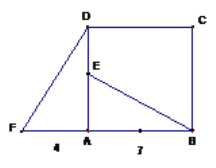
(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
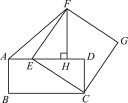
【题目】如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)当AE为何值时,△AEF的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE,则下列结论:①∠DAE=∠BAC;②AE=BE;③AD=AE;④四边形ACBD是平行四边形,其中不正确的是__________.(只填序号)
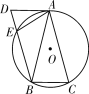
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com