
【题目】如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE,则下列结论:①∠DAE=∠BAC;②AE=BE;③AD=AE;④四边形ACBD是平行四边形,其中不正确的是__________.(只填序号)
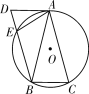
【答案】②
【解析】
利用弦切角与圆周角关系可知∠DAE=∠ABE;BD∥AC可知∠ABE=∠BAC,得证①成立,利用圆内接四边形知识和三角形内角和180°,证明相关角的等量关系,证明线段的数量与位置关系.
∵AD是⊙O的切线,
∴∠DAE=∠ABD.
∵BD∥AC,
∴∠CAB=∠ABD,
∴∠DAE=∠CAB,故①正确;
∵四边形AEBC内接于⊙O,
∴∠AED=∠ACB.
∴△ADE∽△ABC,
∴![]() ,∠ABC=∠ADE,
,∠ABC=∠ADE,
由AB=AC,得AD=AE,故③正确;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ADE=∠ACB,
∴DE∥AC,
∴∠DBA=∠BAC,
∴在△BAD和△ABC中,∠ADE=∠ACB,∠DBA=∠BAC,AB=AB,
∴△BAD≌△ABC,
∴AC=BD,
∴四边形ACBD是平行四边形,故④正确.
②无法得到,故错误.
故答案为:②


科目:初中数学 来源: 题型:
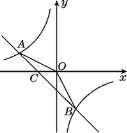
【题目】已知一次函数y=kx+b和反比例函数y=![]() 图象相交于A(-4,2),B(n,-4)两点.
图象相交于A(-4,2),B(n,-4)两点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b-![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
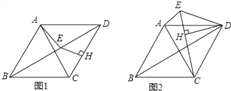
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示.该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.
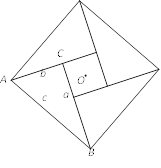
(1)请利用这个图形证明勾股定理;
(2)请利用这个图形说明a2+b2≥2ab,并说明等号成立的条件;
(3)请根据(2)的结论解决下面的问题:长为x,宽为y的长方形,其周长为8,求当x,y取何值时,该长方形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,GH∥AB.分别交AB、CD、AD、BC于E、F、G、H,连接PB.若AE=3,PF=8.则图中阴影部分的面积为( )
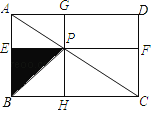
A.8B.12C.16D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
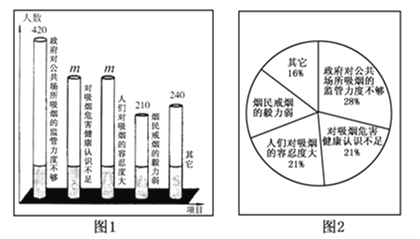
【题目】5月31日是世界无烟日,某卫生机构为了了解“导致吸烟人比例高的最主要原因”,随机抽样调查了该市部分18~65岁的市,民,下图是根据调查结果绘制的统计图,根据图中信息解答下列问题:
(1)这次接受随机抽样调查的市民总人数为 ;
(2)图1中m 的值是 ;
(3)求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数;
(4)若该市18~65岁的市民约有200万人,请你估算其中认为导致吸烟人口比例高的最主要原因是“对吸烟危害健康认识不足”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC,AB=CB,将△ABC绕A点旋转的度数为a(45°<a<180°),连接BD交AC于F,AH平分∠CAD交BD于点H,若△FHA为等腰三角形,则a=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com