
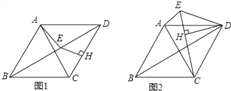
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
【答案】(1) EH2+CH2=AE2;(2)见解析.
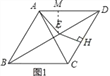
【解析】分析:(1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
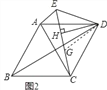
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
详解:
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
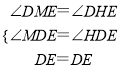 ,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
 ,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
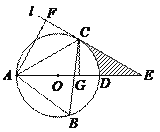
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7
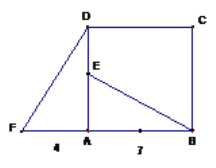
(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
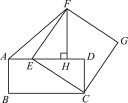
【题目】如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)当AE为何值时,△AEF的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
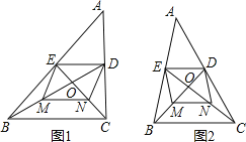
【题目】在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE交于点O.
(1)如图1,若M、N分别是OB、OC的中点,求证:OB=2OD;
(2)如图2,若BD⊥CE,AB=8,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交
AB于G,连接DG,现在有如下4个结论:①![]() ≌
≌![]() ;②
;②![]() ;③∠GDE=45°;④
;③∠GDE=45°;④
DG=DE在以上4个结论中,正确的共有( )个
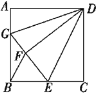
A. 1个 B. 2 个 C. 3 个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE,则下列结论:①∠DAE=∠BAC;②AE=BE;③AD=AE;④四边形ACBD是平行四边形,其中不正确的是__________.(只填序号)
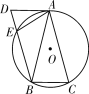
查看答案和解析>>
科目:初中数学 来源: 题型:
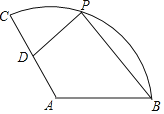
【题目】如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为弧BC上一动点(不与C,B重合),则2PD+PB的最小值为( )
A. ![]() B.
B. ![]() C. 10 D.
C. 10 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com