
【题目】如图,在等腰△ABC中,AB=AC=10,高BD=8,AE平分∠BAC,则△ABE的面积为________.
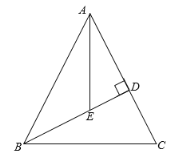
【答案】15.
【解析】
延长AE交BC于点F,过E点作GE![]() AB.在Rt△ADB中,根据勾股定理得到AD,进一步得到CD;在Rt△BDC中,根据勾股定理得到BC;根据等腰三角形的性质和角平分线的性质得到CF,在Rt△AFC中,根据勾股定理得到AF,通过AA证明△DAE∽△FAC,根据相似三角形的性质求解CE,根据角平分线的性质可得GE=DE,然后即可求解△ABE的面积.
AB.在Rt△ADB中,根据勾股定理得到AD,进一步得到CD;在Rt△BDC中,根据勾股定理得到BC;根据等腰三角形的性质和角平分线的性质得到CF,在Rt△AFC中,根据勾股定理得到AF,通过AA证明△DAE∽△FAC,根据相似三角形的性质求解CE,根据角平分线的性质可得GE=DE,然后即可求解△ABE的面积.
解:延长AE交BC于点F,过E点作GE![]() AB
AB
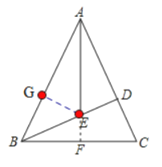
∵在△ABC中,AB=AC=3,高BD=8,
∴在Rt△ADB中,AD=![]() =6,
=6,
∴CD=AC-AD=4,
∴在Rt△BDC中,BC=![]() ,
,
∵AE平分∠BAC,
∴EG=DE,CF=![]() BC=
BC=![]() ,∠AFC=90°,
,∠AFC=90°,
∴在Rt△AFC中,AF=![]() =
=![]() ,
,
∵∠DAE=∠FAC,∠ADE=∠AFC=90°,
∴△DAE∽△FAC,
∴DE:AD=CF:AF,
![]()
∴EG=DE=3
∴SABE=![]()
故答案为:15.


科目:初中数学 来源: 题型:
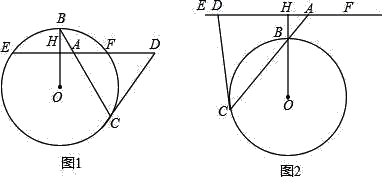
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整的统计图.
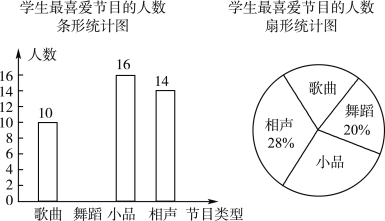
请你根据图中信息,回答下列问题:
(1)求本次调查的学生人数,并补全条形统计图;
(2)在扇形统计图中,求“歌曲”所在扇形的圆心角的度数;
(3)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
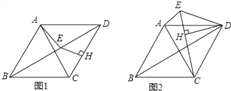
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示.该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.
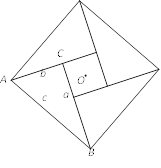
(1)请利用这个图形证明勾股定理;
(2)请利用这个图形说明a2+b2≥2ab,并说明等号成立的条件;
(3)请根据(2)的结论解决下面的问题:长为x,宽为y的长方形,其周长为8,求当x,y取何值时,该长方形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耒阳市某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
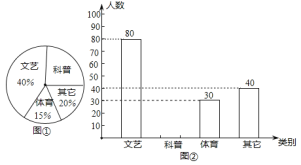
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为 ;
(2)补全条形图;
(3)求在扇形统计图中,喜欢“科普书籍”的所占的圆心角度数;
(4)如果全校共有学生1500名,请估计该校最喜欢“科普”书籍的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com