
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半.
∵AB=AC,∠BAC=90°,点P是BC的中点,
∴AP⊥BC,AP=PC,∠EAP=∠C=45°,
∴∠APF+∠CPF=90°,
∵∠EPF是直角,
∴∠APF+∠APE=90°,
∴∠APE=∠CPF,
在△APE和△CPF中,
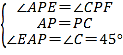 ,
,
∴△APE≌△CPF(ASA),
∴AE=CF,故①②正确;
∵△AEP≌△CFP,同理可证△APF≌△BPE,
∴△EFP是等腰直角三角形,故③错误;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=![]() S△ABC.故④正确,
S△ABC.故④正确,
故选C.


科目:初中数学 来源: 题型:
【题目】用反证法证明命题“在一个三角形中,至少有一个内角小于或等于![]() ”的过程如下:
”的过程如下:
已知: ![]() ;
;
求证: ![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
证明:假设![]() 中没有一个内角小于或等于
中没有一个内角小于或等于![]() ,即
,即![]() ,则
,则
![]() ,
,
这与“__________” 这个定理相矛盾,
所以![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
在证明过程中,横线上应填入的句子是( )
A.三角形内角和等于![]() B.三角形的一个外角等于与它不相邻的两个内角的和
B.三角形的一个外角等于与它不相邻的两个内角的和
C.等边三角形的各角都相等,并且每个角都等于![]() D.等式的性质
D.等式的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:

![]()
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表.设分配给甲店A型产品![]() 件,这家公司卖出这100件产品的总利润为W(元).
件,这家公司卖出这100件产品的总利润为W(元).

(1)求W关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案?
(3)实际销售过程中,公司发现这批产品尤其是A型产品很畅销,便决定对甲店的最后21件A型产品每件提价![]() 元销售(
元销售(![]() 为正整数).两店全部销售完毕后结果的总利润为18000元,求
为正整数).两店全部销售完毕后结果的总利润为18000元,求![]() 值.并写出公司这100件产品对甲乙两店是如何分配的?
值.并写出公司这100件产品对甲乙两店是如何分配的?
查看答案和解析>>
科目:初中数学 来源: 题型:
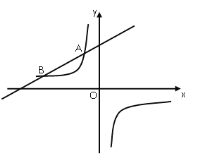
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:

(1)求y与x之间的函数关系式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、![]() 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在![]() 中,两边长分别为
中,两边长分别为![]() ,且且
,且且![]() ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:Rt![]() 中,
中,![]() ,且b>a,若Rt
,且b>a,若Rt![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com