
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标代入即可求得抛物线的解析式.
的坐标代入即可求得抛物线的解析式.
![]() 作BH⊥AC于点H,求出
作BH⊥AC于点H,求出![]() 的长度,即可求出∠ACB的度数.
的长度,即可求出∠ACB的度数.
![]() 延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线
延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线![]() 的方程,和抛物线的方程联立即可求得点
的方程,和抛物线的方程联立即可求得点![]() 的坐标.
的坐标.
试题解析:(1)由题意,得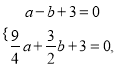
解得![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(![]() ,0),
,0),
∴AC=![]() ,AB=
,AB=![]() ,OC=3,BC=
,OC=3,BC=![]() .
.
∵![]() ,即∠BAD=
,即∠BAD= ![]() ,
,
∴![]() .
.
Rt△ BCH中, ![]() ,BC=
,BC=![]() ,∠BHC=90,
,∠BHC=90,
∴![]() .
.
又∵∠ACB是锐角,∴![]() .
.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=![]() ,
,
∴![]() .
.
∵△DCE∽△AOC,∴只可能∠CAO=∠DCE.
∴AG = CG.
∴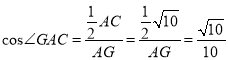 .
.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴![]() .
.
∴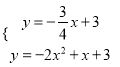 解得
解得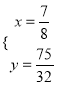 ,
, ![]() (舍).
(舍).
∴点D坐标是![]()


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明同学积极响应学校号召,利用假期参加了班级组织的“研学旅行”活动,在参观某红色景区时,李明站在台阶DF上发现了对面山坡BC上有一块竖立的标语牌AB,他在台阶顶端F处测得标语牌顶点A的仰角为![]() ,标语牌底端B的仰角为
,标语牌底端B的仰角为![]() ,如图,已知台阶高EF为3米,山坡坡面BC的长为25米,山坡BC的坡度为1:
,如图,已知台阶高EF为3米,山坡坡面BC的长为25米,山坡BC的坡度为1:![]() ,求标语牌AB的高度
,求标语牌AB的高度![]() 结果精确到
结果精确到![]() 米,参考数据
米,参考数据![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )

A.30 B.33 C.36 D.39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等、四内角相等)中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=3,则EF的平方为( )

A.2B.![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,在长方形OABC中,OC∥AB,OA∥BC,两边OC、OA分别在x轴和y轴上,且点B(a,b)满足:![]() +(2b+6)2=0.
+(2b+6)2=0.
(1)求点B的坐标;
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:3两部分,求点P的坐标;
(3)如图2,M为线段OC一点,且∠ABM=∠AMB,N是x轴负半轴上一动点,∠MAN的平分线AD交BM的延长线于点D,在点N运动的过程中,试判断∠ANM与∠D的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com