
����Ŀ����ͼ����OΪƽ��ֱ������ϵ��ԭ�㣬�ڳ�����OABC�У�OC��AB��OA��BC������OC��OA�ֱ���x���y���ϣ��ҵ�B��a��b�����㣺![]() +��2b+6��2=0��
+��2b+6��2=0��
��1�����B�����ꣻ
��2����ͼ1��������B��ֱ��BP�볤����OABC�ı߽��ڵ�P���ҽ�������OABC�������Ϊ1��3�����֣����P�����ꣻ
��3����ͼ2��MΪ�߶�OCһ�㣬����ABM=��AMB��N��x�Ḻ������һ���㣬��MAN��ƽ����AD��BM���ӳ����ڵ�D���ڵ�N�˶��Ĺ����У����ж���ANM����D��������ϵ����˵�����ɣ�

���𰸡���1��B��4����3����2����2��0����0����![]() ����3����ANM=2��D
����3����ANM=2��D
��������
��1�����÷Ǹ��������ʼ��ɽ�����⣻
��2�����������ηֱ�������⼴�ɣ�
��3�����ۣ���ANM=2��D����ME��AD��AB��E���ӳ�BA��F������ƽ���ߵ����ʣ���ƽ���ߵĶ��弴�ɽ�����⣻
��1�������⣺4��a=0��2b+6=0��
��a=4��b=��3��
��B��4����3����
��2��������P��OC��ʱ�������⣺S��BCP��S�ı���OABC=1��4��
��![]() CP3=
CP3=![]() ��3��4��
��3��4��
��PC=2��
��OP=4��2=2��
��P��2��0����
������P��OA��ʱ��S��ABP=![]() S�ı���OABC��
S�ı���OABC��
��![]() PA4=
PA4=![]() ��3��4
��3��4
��PA=![]() ��
��
��OP=3��![]() =
=![]() ��
��
��P��0����![]() ����
����
�������������������ĵ�P����Ϊ��2��0����0����![]() ����
����
��3�����ۣ���ANM=2��D��
���ɣ���ME��AD��AB��E���ӳ�BA��F��
��ME��AD��
���1=��D����2=��3��
��ADƽ����MAN��
���MAN=2��3��
��OC��AB��
���ABM=��CMB��
�ߡ�AMB=��CMB��
���AMC=2��AMB��
��OC��AB��
���FAM=��AMC=2��AMB��
���ANM=2��AMB��2��3
=2��AMB��2��2
=2����AMB����2��
=2��1
=2��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������A��
������A��![]() ��0����B��
��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE����AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����PΪ���ǡ�AOB��ƽ�����ϵ�һ�����㣬�ҡ�MPN���AOB����������MPN���Ƶ�P��ת�Ĺ����У������߷ֱ���OA��OB�ཻ��M��N���㣬�����½��ۣ���1��PM��PN���������2��OM��ON��ֵ���䣬��3���ı���PMON��������䣬��4��MN�ij����䣬
������ȷ��Ϊ__________������д����ǰ�����ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ���ϣ�����ʦ��ʾ��һ����Ŀ������ͼ��ABCD�ĶԽ����ཻ�ڵ�O������O��EF��ֱ��BD��AB��CD�ֱ��ڵ�F��E������DF��BE�����������������д��һ����ȷ���ۣ���������λͬѧд���Ľ������£�
С�ࣺOE=OF��С�Σ��ı���DFBE�������Σ�
С�ģ�S�ı���AFED=S�ı���FBCE��С�꣺��ACE=��CAF��
����λͬѧд���Ľ����в���ȷ���ǣ�������

A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֤���������Խ�����ȵ�ƽ���ı����Ǿ�������Ҫ�������⣬����ͼ�Σ����÷��ű�ʾ��֪����֤��д��֤�����̣�������С��ͬѧ�������⻭����ͼ�Σ���д���˲���������֪����֤��
��֪����ͼ��ABCD��ƽ���ı��Σ�AC��BD�ǶԽ��ߣ����� ����
��֤���� ����
���㲹ȫ��֪����֤����д��֤�����̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AC��ȡ��B������ͬһ���������ȱ���������ABD ����BCE ������AE��CD��GF�����н�����ȷ���У� ��

�� AE DC����AHC120������AGB�ա�DFB����BHƽ��AHC����GF��AC
A.�٢ڢ�B.�٢ۢ�C.�٢ۢܢ�D.�٢ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ִ���A�۳�������28����/Сʱ���ٶ������������У���ʱ��ĵ���M�ڱ�ƫ��30���ķ����ϣ���Сʱ���ִ�����B������ʱ��õ���M�ڱ�ƫ��60���ķ����ϣ�
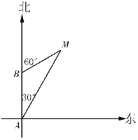
��1�����ִ���B��ʱ�����M�ľ��룻
��2���ִ���B�����������������У��־���Сʱ��C������ʱ�ִ������M�ľ����Ƕ��٣�����M���ִ���ʲô�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����������ת����ת���У�ָ��λ�ù̶����������ε��������ȣ��ҷֱ��������1��2��3��

��1��С��ת��ת��һ�Σ���ת��ֹͣת��ʱ��ָ����ָ�����е������������ĸ���Ϊ________��
��2��С����ת��ת��һ�Σ���ת��ֹͣת��ʱ����¼��ָ����ָ�����е����֣�������ת��ת��һ�Σ���ת��ֹͣת��ʱ���ٴμ�¼��ָ����ָ�����е����֣�������������֮����3�ı����ĸ���(�û���״ͼ���б��ȷ������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ�����ͼ���㣨��![]() ����
����![]() ������ͼ����x��Ľ��㵽ԭ��ľ���Ϊ1�����һ�κ����Ľ���ʽΪ��_____��
������ͼ����x��Ľ��㵽ԭ��ľ���Ϊ1�����һ�κ����Ľ���ʽΪ��_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com