
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA,OB相交于M、N两点,则以下结论:(1)PM=PN恒成立,(2)OM+ON的值不变,(3)四边形PMON的面积不变,(4)MN的长不变,
其中正确的为__________(请填写结论前面的序号).

【答案】(1)(2)(3)
【解析】
如图作PE⊥OA于E,PF⊥OB于F.只要证明△POE≌△POF,△PEM≌△PFN,即可一一判断.
如图作PE⊥OA于E,PF⊥OB于F.
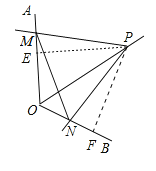
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在△POE和△POF中,
![]() ,
,
∴△POE≌△POF,
∴OE=OF,
在△PEM和△PFN中,
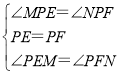 ,
,
∴△PEM≌△PFN,
∴EM=NF,PM=PN,故(1)正确,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故(3)正确,
∵OM+ON=OE+ME+OF-NF=2OE=定值,故(2)正确,
MN的长度是变化的,故(4)错误,
故答案是: (1)(2)(3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )

A.30 B.33 C.36 D.39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等、四内角相等)中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=3,则EF的平方为( )

A.2B.![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列结论中:①有三个角是![]() 的三角形是等边三角形;②有一个外角是
的三角形是等边三角形;②有一个外角是![]() 的等腰三角形是等边三角形;③有一个角是
的等腰三角形是等边三角形;③有一个角是![]() ,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是__________.
,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.
(1)AC= cm;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,在长方形OABC中,OC∥AB,OA∥BC,两边OC、OA分别在x轴和y轴上,且点B(a,b)满足:![]() +(2b+6)2=0.
+(2b+6)2=0.
(1)求点B的坐标;
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:3两部分,求点P的坐标;
(3)如图2,M为线段OC一点,且∠ABM=∠AMB,N是x轴负半轴上一动点,∠MAN的平分线AD交BM的延长线于点D,在点N运动的过程中,试判断∠ANM与∠D的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=90°,
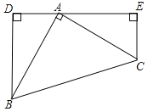
(1)△ABD≌△CAE
(2)探索DE、BD、CE长度之间的关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com