
ЁОЬтФПЁПФГаЃзщжЏвЛЯюЙЋвцжЊЪЖОКШќЃЌБШШќЙцЖЈЃКУПИіАрМЖгЩ2УћФаЩњЁЂ2УћХЎЩњМА1УћАржїШЮРЯЪІзщГЩДњБэЖгЃЎЕЋВЮШќЪБЃЌУПАржЛФмга3УћЖгдБЩЯГЁВЮШќЃЌАржїШЮРЯЪІБиаыВЮМгЃЌСэЭт2УћЖгдБЗжБ№дк2УћФаЩњКЭ2УћХЎЩњжаИїЫцЛњГщГі1УћЃЎГѕШ§ЃЈ1ЃЉАргЩМзЁЂвв2УћФаЩњКЭБћЁЂЖЁ2УћХЎЩњМА1УћАржїШЮзщГЩСЫДњБэЖгЃЌЧѓЧЁКУГщЕНгЩФаЩњМзЁЂХЎЩњБћКЭетЮЛАржїШЮвЛЦ№ЩЯГЁВЮШќЕФИХТЪЃЎЃЈЧыгУЁАЛЪїзДЭМЁБЛђЁАСаБэЁБЛђЁАСаОйЁБЕШЗНЗЈИјГіЗжЮіЙ§ГЬЃЉ
ЁОД№АИЁП![]() .
.
ЁОНтЮіЁП
СаБэЕУГіЫљгаЕШПЩФмЕФЧщПіЪ§ЃЌевГіГщЕНгЩФаЩњМзЁЂХЎЩњБћКЭетЮЛАржїШЮвЛЦ№ЩЯГЁВЮШќЕФЧщПіЪ§ЃЌМДПЩЧѓГіЫљЧѓЕФИХТЪЃЎ
ЩшФаЭЌбЇБъМЧЮЊAЁЂBЃЛХЎбЇЩњБъМЧЮЊ1ЁЂ2ЃЌПЩФмГіЯжЕФЫљгаНсЙћСаБэШчЯТЃК
Мз | вв | Бћ | ЖЁ | |
Мз | / | ЃЈввЃЌМзЃЉ | ЃЈБћЃЌМзЃЉ | ЃЈЖЁЃЌМзЃЉ |
вв | ЃЈМзЃЌввЃЉ | / | ЃЈБћЃЌввЃЉ | ЃЈЖЁЃЌввЃЉ |
Бћ | ЃЈМзЃЌБћЃЉ | ЃЈввЃЌБћЃЉ | / | ЃЈЖЁЃЌБћЃЉ |
ЖЁ | ЃЈМзЃЌЖЁЃЉ | ЃЈввЃЌЖЁЃЉ | ЃЈБћЃЌЖЁЃЉ | / |
ЙВга12жжПЩФмЕФНсЙћЃЌЧвУПжжЕФПЩФмадЯрЭЌЃЌЦфжаЧЁКУГщЕНгЩФаЩњМзЁЂХЎЩњБћКЭетЮЛАржїШЮвЛЦ№ЩЯГЁВЮШќЕФНсЙћга2жжЃЌ
ЫљвдЧЁКУГщЕНгЩФаЩњМзЁЂХЎЩњБћКЭетЮЛАржїШЮвЛЦ№ЩЯГЁВЮШќЕФИХТЪЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЗНГЬзщ![]() ЕФНтxЮЊЗЧе§Ъ§ЃЌyЮЊИКЪ§ЃЎ
ЕФНтxЮЊЗЧе§Ъ§ЃЌyЮЊИКЪ§ЃЎ
(1)ЧѓaЕФШЁжЕЗЖЮЇЃЛ
(2)ЛЏМђ|aЃ3|ЃЋ|aЃЋ2|ЃЛ
(3)дкaЕФШЁжЕЗЖЮЇжаЃЌЕБaЮЊКЮећЪ§ЪБЃЌВЛЕШЪН2axЃЋxЃО2aЃЋ1ЕФНтЮЊxЃМ1.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЊЪЖзМБИ:Ъ§жсЩЯ![]() СНЕуЖдгІЕФЪ§ЗжБ№ЮЊ
СНЕуЖдгІЕФЪ§ЗжБ№ЮЊ![]() ЃЎдђ
ЃЎдђ![]() СНЕужЎМфЕФОрРыБэЪОЮЊ:
СНЕужЎМфЕФОрРыБэЪОЮЊ:![]()
ЮЪЬтЬНОП:Ъ§жсЩЯ![]() СНЕуЖдгІЕФЪ§ЗжБ№ЮЊ
СНЕуЖдгІЕФЪ§ЗжБ№ЮЊ![]() Чв
Чв![]() Тњзу
Тњзу![]()
![]() жБНгаДГі:
жБНгаДГі:![]() ___ЁЂ
___ЁЂ![]()
![]() дкЪ§жсЩЯгавЛЕу
дкЪ§жсЩЯгавЛЕу![]() ЖдгІЕФЪ§ЮЊ
ЖдгІЕФЪ§ЮЊ![]() ЃЌЧыЮЪ:ЕБЕу
ЃЌЧыЮЪ:ЕБЕу![]() ЕН
ЕН![]() СНЕуЕФОрРыКЭЮЊ
СНЕуЕФОрРыКЭЮЊ![]() ЪБ,
ЪБ,![]() ТњзуЪВУДЬѕМў?ЧыРћгУЪ§жсНјааЫЕУї(ДЫЪБ
ТњзуЪВУДЬѕМў?ЧыРћгУЪ§жсНјааЫЕУї(ДЫЪБ![]() зюаЁ)ЃЎ
зюаЁ)ЃЎ
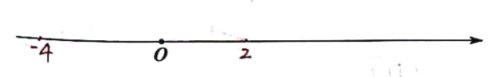
ЭиеЙ:ЕБЪ§жсЩЯ гІгУ:ЙњЧьЦкМфККПкНЬВЮфККЙижСГЄНЖўЧХжЎМфЪЧЙлПДЁА70жмФъЙњЧьЕЦЙтауЁБЕФРэЯыЧјгђ,ЮфККЙигыГЄНЖўЧХЯрОрдМ![]() Ш§ЕуЖдгІЕФЪ§ЗжБ№ЮЊ
Ш§ЕуЖдгІЕФЪ§ЗжБ№ЮЊ![]() дкЪ§жсЩЯгавЛЕу
дкЪ§жсЩЯгавЛЕу![]() ЖдгІЕФЪ§ЮЊ
ЖдгІЕФЪ§ЮЊ![]() ,ЕБ
,ЕБ![]() ТњзуЪВУДЬѕМўЪБ,
ТњзуЪВУДЬѕМўЪБ,![]() ЕФжЕзюаЁ?
ЕФжЕзюаЁ? 
![]() ЙЋРяЁЃдкЙњЧьЦкМф,ЮЊСЫЗўЮёЙуДѓЪаУё,ККПкНЬВЙмРэДІдкККПкНЬВЮфККЙижСГЄНЖўЧХжЎМфУПИє
ЙЋРяЁЃдкЙњЧьЦкМф,ЮЊСЫЗўЮёЙуДѓЪаУё,ККПкНЬВЙмРэДІдкККПкНЬВЮфККЙижСГЄНЖўЧХжЎМфУПИє![]() ЙЋРяАВХХСЫБуУёЗўЮёаЁзщ(ЮфККЙигыГЄНЖўЧХВЛАВХХ) ,ЛЙашвЊЩшжУвЛИіБуУёЗўЮёЮязЪеО,ЧыЮЪБуУёЗўЮёЮязЪеОгІИУЩшжУдкЪВУДЕиЗН,ЪЙЫќЕНИїИіБуУёЗўЮёаЁзщЕФОрРыКЭзюаЁЃЌзюаЁжЕЪЧЖрЩйЙЋРя?БуУёЗўЮёЮязЪеОЮЛжУДњБэЕФЪ§МЧзї
ЙЋРяАВХХСЫБуУёЗўЮёаЁзщ(ЮфККЙигыГЄНЖўЧХВЛАВХХ) ,ЛЙашвЊЩшжУвЛИіБуУёЗўЮёЮязЪеО,ЧыЮЪБуУёЗўЮёЮязЪеОгІИУЩшжУдкЪВУДЕиЗН,ЪЙЫќЕНИїИіБуУёЗўЮёаЁзщЕФОрРыКЭзюаЁЃЌзюаЁжЕЪЧЖрЩйЙЋРя?БуУёЗўЮёЮязЪеОЮЛжУДњБэЕФЪ§МЧзї![]() РћгУЯТЭМжБНгИјГіНсЙћ:
РћгУЯТЭМжБНгИјГіНсЙћ:![]() ТњзуЕФЬѕМў: зюаЁжЕЮЊ ЙЋРяЃЎ
ТњзуЕФЬѕМў: зюаЁжЕЮЊ ЙЋРяЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,е§ЗНаЮABCDЕФУцЛ§ЮЊ12,ЁїABCЪЧЕШБпШ§НЧаЮ,ЕуEдке§ЗНаЮABCDФк,ЖдНЧЯпACЩЯгавЛЕуPЪЙPE+PDЕФКЭзюаЁ,етИізюаЁжЕЮЊ( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌAB=10ЃЌAC=2![]() ЃЌЁЯB=30ЁуЃЌдђЁїABCЕФУцЛ§ЕШгк_____ЃЎ
ЃЌЁЯB=30ЁуЃЌдђЁїABCЕФУцЛ§ЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдНЧЯпГЄЗжБ№ЮЊ6КЭ8ЕФСтаЮABCDШчЭМЫљЪОЃЌЕуOЮЊЖдНЧЯпЕФНЛЕуЃЌЙ§ЕуOелЕўСтаЮЃЌЪЙBЃЌBЁфСНЕужиКЯЃЌMNЪЧелКлЃЎШєB'M=1ЃЌдђCNЕФГЄЮЊЃЈЁЁЁЁЃЉ
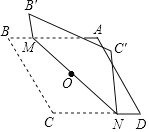
A. 7 B. 6 C. 5 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЖЅЕуBЕФзјБъЮЊ(8ЃЌ3)ЃЌЖЈЕуDЕФзјБъЮЊ(12ЃЌ0)ЃЌЖЏЕуPДгЕуCГіЗЂЃЎвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиCBдШЫйдЫЖЏЃЌЖЏЕуQДгЕуDГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсЕФИКЗНЯђдШЫйдЫЖЏЃЌPЃЌQСНЕуЭЌЪБдЫЖЏЃЌЕБQЕуЕНДяOЕуЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtУыЃЌ
(1)ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮOCPQЮЊОиаЮЃП
(2)ЕБtЮЊКЮжЕЪБЃЌвдCЃЌPЃЌQЃЌAЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃП
(3)EЕузјБъ(5ЃЌ0)ЃЌЕБЁїOEPЮЊЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌBCЃНBDЃЌADЃНDEЃНEBЃЌдђЁЯAЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
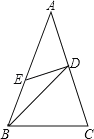
A.30ЁуB.36ЁуC.45ЁуD.50Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпC1ЃКy=ax2Љ2ax+cЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЎвбжЊЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуOЮЊзјБъдЕуЃЌOC=3OAЃЌХзЮяЯпC1ЕФЖЅЕуЮЊGЃЎ

ЃЈ1ЃЉЧѓГіХзЮяЯпC1ЕФНтЮіЪНЃЌВЂаДГіЕуGЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋХзЮяЯпC1ЯђЯТЦНвЦkЃЈkЃО0ЃЉИіЕЅЮЛЃЌЕУЕНХзЮяЯпC2ЃЌЩшC2гыxжсЕФНЛЕуЮЊAЁфЁЂBЁфЃЌЖЅЕуЮЊGЁфЃЌЕБЁїAЁфBЁфGЁфЪЧЕШБпШ§НЧаЮЪБЃЌЧѓkЕФжЕЃК
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ3ЃЌЩшЕуMЮЊxжсе§АыжсЩЯвЛЖЏЕуЃЌЙ§ЕуMзїxжсЕФДЙЯпЗжБ№НЛХзЮяЯпC1ЁЂC2гкPЁЂQСНЕуЃЌЪдЬНОПдкжБЯпy=Љ1ЩЯЪЧЗёДцдкЕуNЃЌЪЙЕУвдPЁЂQЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOQШЋЕШЃЌШєДцдкЃЌжБНгаДГіЕуMЃЌNЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com