
【题目】已知△ABC中,AB=10,AC=2![]() ,∠B=30°,则△ABC的面积等于_____.
,∠B=30°,则△ABC的面积等于_____.
【答案】15![]() 或10
或10![]()
【解析】作AD⊥BC交BC(或BC延长线)于点D,分AB、AC位于AD异侧和同侧两种情况,先在Rt△ABD中求得AD、BD的值,再在Rt△ACD中利用勾股定理求得CD的长,继而就两种情况分别求出BC的长,根据三角形的面积公式求解可得.
作AD⊥BC交BC(或BC延长线)于点D,
①如图1,当AB、AC位于AD异侧时,
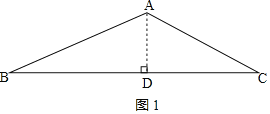
在Rt△ABD中,∵∠B=30°,AB=10,
∴AD=ABsinB=5,BD=ABcosB=5![]() ,
,
在Rt△ACD中,∵AC=2![]() ,
,
∴CD=![]() ,
,
则BC=BD+CD=6![]() ,
,
∴S△ABC=![]() BCAD=
BCAD=![]() ×6
×6![]() ×5=15
×5=15![]() ;
;
②如图2,当AB、AC在AD的同侧时,
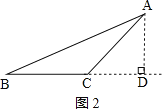
由①知,BD=5![]() ,CD=
,CD=![]() ,
,
则BC=BD-CD=4![]() ,
,
∴S△ABC=![]() BCAD=
BCAD=![]() ×4
×4![]() ×5=10
×5=10![]() .
.
综上,△ABC的面积是15![]() 或10
或10![]() ,
,
故答案为15![]() 或10
或10![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴分别交于原点
轴分别交于原点![]() 和点
和点![]() ,与对称轴
,与对称轴![]() 交于点
交于点![]() .矩形
.矩形![]() 的边
的边![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,边
,边![]() ,
,![]() 与抛物线分别交于点
与抛物线分别交于点![]() ,
,![]() .当矩形
.当矩形![]() 沿
沿![]() 轴正方向平移,点
轴正方向平移,点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的同侧时,连接
的同侧时,连接![]() ,此时,四边形
,此时,四边形![]() 的面积记为
的面积记为![]() ;点
;点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的两侧时,连接
的两侧时,连接![]() ,
,![]() ,此时五边形
,此时五边形![]() 的面积记为
的面积记为![]() .将点
.将点![]() 与点
与点![]() 重合的位置作为矩形
重合的位置作为矩形![]() 平移的起点,设矩形
平移的起点,设矩形![]() 平移的长度为
平移的长度为![]() .
.
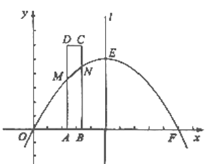
(1)求出这条抛物线的表达式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当矩形![]() 沿着
沿着![]() 轴的正方向平移时,求
轴的正方向平移时,求![]() 关于
关于![]() 的函数表达式,并求出
的函数表达式,并求出![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的两条对角线AC、BD互相垂直, A1B1C1D1, 是四边形ABCD的中点四边形,如果AC=8, BD=10,那么四边形A1B1C1D1,的面积为_________.
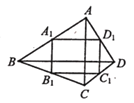
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com