
【题目】知识准备:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() .则
.则![]() 两点之间的距离表示为:
两点之间的距离表示为:![]()
问题探究:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 且
且![]() 满足
满足![]()
![]() 直接写出:
直接写出:![]() ___、
___、![]()
![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,请问:当点
,请问:当点![]() 到
到![]() 两点的距离和为
两点的距离和为![]() 时,
时,![]() 满足什么条件?请利用数轴进行说明(此时
满足什么条件?请利用数轴进行说明(此时![]() 最小).
最小).
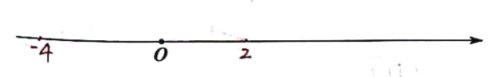
拓展:当数轴上 应用:国庆期间汉口江滩武汉关至长江二桥之间是观看“70周年国庆灯光秀”的理想区域,武汉关与长江二桥相距约![]() 三点对应的数分别为
三点对应的数分别为![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,当
,当![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?
的值最小? 
![]() 公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔
公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔![]() 公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作
公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作![]() 利用下图直接给出结果:
利用下图直接给出结果:![]() 满足的条件: 最小值为 公里.
满足的条件: 最小值为 公里.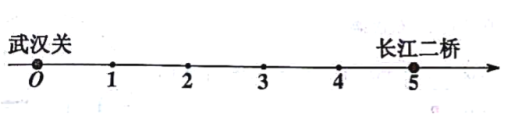
【答案】问题探究:(1)![]() ,
,![]() ; (2)
; (2)![]() ;拓展:当
;拓展:当![]() 时,
时,![]() 最小时为
最小时为![]() ;应用:
;应用:![]() ;4
;4
【解析】
问题探究:
(1)根据非负数的性质可得![]() 和
和![]() 的值;
的值;
(2)根据绝对值的几何意义,可得当点P在AB之间(包括A,B两点),P到A点与P到B点的距离之和是6,即PA+PB最小;
拓展:点P在点A和点B(含点A和点B)之间,依此即可求解.
应用:同理根据拓展的问题,分情况即可求解.
问题探究:
(1)∵![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)如图1,

点P到A、B两点的距离和为6时,点P在AB之间(包括A,B两点),即![]() ,此时PA+PB最小;
,此时PA+PB最小;
拓展:

点P表示的数为2,该最小值为12,
设P到A、B、C的距离和为d,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() >12,
>12,
④当x>8时![]() >18;
>18;
综上,当点P表示的数为2时,P到A、B、C的距离和最小,最小值为12.
应用:
如图3,设便民服务物资站为点P,各便民服务小组分别为A,B,C,D,
设P到A、B、C、D的距离和为d,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() >4,
>4,
③当![]() 时,
时,![]() ,
,
④当![]() 时,
时,![]() >4,
>4,
⑤当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
综上,![]() 满足的条件:
满足的条件:![]() ,最小值为4公里.
,最小值为4公里.
故答案为:![]() ,4.
,4.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
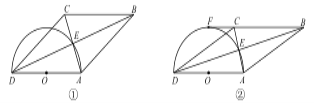
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
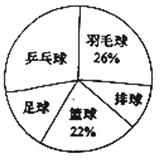
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
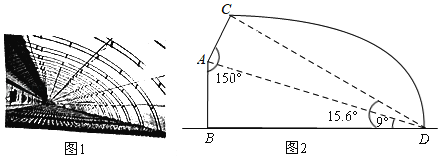
【题目】随着我市农产品整体品牌形象“聊胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段AB,BD分别表示大棚的墙高和跨度,AC表示保温板的长.已知墙高AB为2米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2.求保温板AC的长是多少米?(精确到0.1米)
(参考数据:![]() ≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴分别交于原点
轴分别交于原点![]() 和点
和点![]() ,与对称轴
,与对称轴![]() 交于点
交于点![]() .矩形
.矩形![]() 的边
的边![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,边
,边![]() ,
,![]() 与抛物线分别交于点
与抛物线分别交于点![]() ,
,![]() .当矩形
.当矩形![]() 沿
沿![]() 轴正方向平移,点
轴正方向平移,点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的同侧时,连接
的同侧时,连接![]() ,此时,四边形
,此时,四边形![]() 的面积记为
的面积记为![]() ;点
;点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的两侧时,连接
的两侧时,连接![]() ,
,![]() ,此时五边形
,此时五边形![]() 的面积记为
的面积记为![]() .将点
.将点![]() 与点
与点![]() 重合的位置作为矩形
重合的位置作为矩形![]() 平移的起点,设矩形
平移的起点,设矩形![]() 平移的长度为
平移的长度为![]() .
.
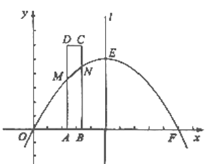
(1)求出这条抛物线的表达式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当矩形![]() 沿着
沿着![]() 轴的正方向平移时,求
轴的正方向平移时,求![]() 关于
关于![]() 的函数表达式,并求出
的函数表达式,并求出![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
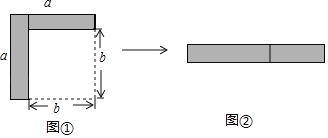
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com