
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为66万元;本周已售出2辆A型车和1辆B型车,销售额为42万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过84万元.问最多可以购买多少辆B型号的新能源汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是个三角形,分别连接这个三角形三边中点得到图2,再分别连接图2中间小三角形三边的中点得到图3.

![]() 图1中有_ __个三角形,图2中有 __个三角形,图3 中有 __个三角形;
图1中有_ __个三角形,图2中有 __个三角形,图3 中有 __个三角形;
![]() 按上面的方法继续下去,第
按上面的方法继续下去,第![]() 个图形有________个三角形;(用含
个图形有________个三角形;(用含![]() 的式子表示)
的式子表示)
![]() 当
当![]() 时,图形中有多少个三角形?
时,图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动,旅行社代办购买动车票,动车票价格如下表所示:
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 65(元) | 54(元) | 40(元) |
根据报名总人数,若所有人员都买一等座的动车票,则共需13650元,若都买二等座动车票(学生全部按表中的“学生票二等座”购买),则共需8820元;已知家长的人数是教师的人数的2倍.
(1)设参加活动的老师有m人,请直接用含m的代数式表示教师和家长购买动车票所需的总费用;
(2)求参加活动的总人数;
(3)如果二等座动车票共买到x张,且学生全部按表中的“学生票二等座”购买 ,其余的买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
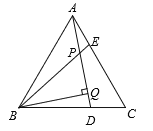
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产![]() 辆,自行车厂平均每天生产自行车
辆,自行车厂平均每天生产自行车![]() 辆,由于各种原因实际每天生产量与计划每天生产量相比有出入,下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)
辆,由于各种原因实际每天生产量与计划每天生产量相比有出入,下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增将 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产自行车 辆;
根据记录可知前三天共生产自行车 辆;
![]() 产量最多的一天比产量最少的一天多生产 辆;
产量最多的一天比产量最少的一天多生产 辆;
![]() 若该厂实行按生产的自行车数量的多少计工资(即计件工资制).如果每生产一辆自行车可得人民币
若该厂实行按生产的自行车数量的多少计工资(即计件工资制).如果每生产一辆自行车可得人民币![]() 元,那么该厂工人这一周的工资总额是多少元.
元,那么该厂工人这一周的工资总额是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识准备:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() .则
.则![]() 两点之间的距离表示为:
两点之间的距离表示为:![]()
问题探究:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 且
且![]() 满足
满足![]()
![]() 直接写出:
直接写出:![]() ___、
___、![]()
![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,请问:当点
,请问:当点![]() 到
到![]() 两点的距离和为
两点的距离和为![]() 时,
时,![]() 满足什么条件?请利用数轴进行说明(此时
满足什么条件?请利用数轴进行说明(此时![]() 最小).
最小).
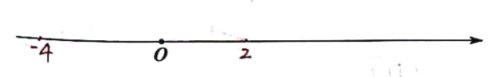
拓展:当数轴上 应用:国庆期间汉口江滩武汉关至长江二桥之间是观看“70周年国庆灯光秀”的理想区域,武汉关与长江二桥相距约![]() 三点对应的数分别为
三点对应的数分别为![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,当
,当![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?
的值最小? 
![]() 公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔
公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔![]() 公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作
公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作![]() 利用下图直接给出结果:
利用下图直接给出结果:![]() 满足的条件: 最小值为 公里.
满足的条件: 最小值为 公里.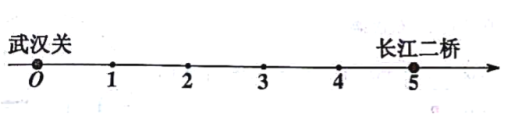
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点C出发.以每秒1个单位长度的速度沿CB匀速运动,动点Q从点D出发,以每秒2个单位长度的速度沿x轴的负方向匀速运动,P,Q两点同时运动,当Q点到达O点时两点同时停止运动.设运动时间为t秒,
(1)当t为何值时,四边形OCPQ为矩形?
(2)当t为何值时,以C,P,Q,A为顶点的四边形为平行四边形?
(3)E点坐标(5,0),当△OEP为等腰三角形时,请直接写出所有符合条件的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com